Khoảng cách giữa đường thẳng, mặt phẳng song song

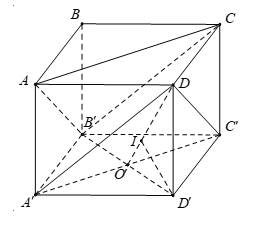
Ta có: \(\left\{ \begin{array}{l}A'C'//AC\\DC'//AB'\end{array} \right. \Rightarrow \left( {A'C'D} \right)//\left( {ACB'} \right)\)

Gọi \(O'\) là tâm của hình vuông $A'B'C'D'$.

Ta có $d\left( {\left( {AB'C} \right),\left( {A'DC'} \right)} \right) = d\left( {B',\left( {A'DC'} \right)} \right) = d\left( {D',\left( {A'DC'} \right)} \right)$

Gọi \(I\) là hình chiếu của \(D'\) trên \(O'D\).

Vì \(D'O' \bot A'C',DO' \bot A'C'\) nên \(A'C' \bot \left( {{\rm{DOD}}'} \right) \Rightarrow A'C' \bot D'I\).

Mà \(D'I \bot DO'\) nên \(I\) là hình chiếu của \(D'\) trên $\left( {A'DC'} \right)$.

$ \Rightarrow d\left( {\left( {AB'C} \right),\left( {A'DC'} \right)} \right) = d\left( {D',\left( {A'DC'} \right)} \right) = D'I = \dfrac{{D'O'.D'D}}{{\sqrt {D'{{O'}^2} + D'{D^2}} }} = \dfrac{{\dfrac{{a\sqrt 2 }}{2}.a}}{{\sqrt {{{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2} + {a^2}} }} = \dfrac{{a\sqrt 3 }}{3}.$

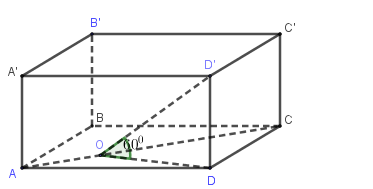
Gọi \(O\)  là hình chiếu của \(D\) lên \(AC\).

Ta có \(\left\{ \begin{array}{l}\left( {ACD'} \right) \cap \left( {ABCD} \right) = AC\\AC \bot DO\\AC \bot D'O\left( {AC \bot \left( {ODD'} \right) \supset OD'} \right)\end{array} \right.\)

\( \Rightarrow \left( {\widehat {\left( {D'AC} \right),\left( {ABCD} \right)}} \right) = \widehat {D'OD} = {60^0}\)

 \(AC = \sqrt {{3^2} + {4^2}}  = 5\) ; \(DO = \dfrac{{AD.DC}}{{AC}} = \dfrac{{12}}{5}\)

Khoảng cách giữa hai mặt đáy là \(DD' = DO.\tan {60^0} = \dfrac{{12\sqrt 3 }}{5}\)

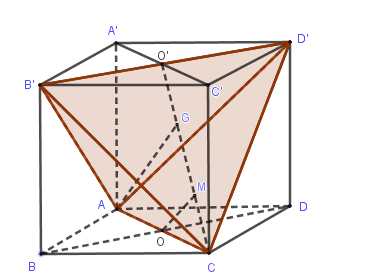
Gọi \(O,O'\) lần lượt là tâm hai đáy \(ABCD,A'B'C'D'\) .

Vì \(BD//B'D'\) nên \(BD//\left( {CB'D'} \right)\).

Do đó \(d\left( {BD,\left( {CB'D'} \right)} \right) = d\left( {O,\left( {CB'D'} \right)} \right) = \dfrac{1}{2}d\left( {A,\left( {CB'D'} \right)} \right)\)

Mà \(AO \cap \left( {CB'D'} \right) = C \Rightarrow d\left( {O,\left( {CB'D'} \right)} \right) = \dfrac{1}{2}d\left( {A,\left( {CB'D'} \right)} \right)\)

Vậy \(d\left( {BD,\left( {CB'D'} \right)} \right) = \dfrac{1}{2}d\left( {A,\left( {CB'D'} \right)} \right)\)

Ta tính \(d\left( {A,\left( {CB'D'} \right)} \right)\).

Xét tứ diện \(ACB'D'\) có \(AB' = AC = AD' = B'C = B'D' = CD' = a\sqrt 2 \) nên nó là tứ diện đều cạnh \(a\sqrt 2 \).

Gọi \(G\) là trọng tâm tam giác \(CB'D'\) thì \(CG = \dfrac{2}{3}CO' = \dfrac{2}{3}.\dfrac{{a\sqrt 2 .\sqrt 3 }}{2} = \dfrac{{a\sqrt 6 }}{3}\)

Do đó \(d\left( {A,\left( {CB'D'} \right)} \right) = AG = \sqrt {A{C^2} - C{G^2}}  = \sqrt {2{a^2} - \dfrac{{6{a^2}}}{9}}  = \dfrac{{2a\sqrt 3 }}{3}\)

Vậy \(d\left( {BD;\left( {CB'D'} \right)} \right) = \dfrac{1}{2}d\left( {A,\left( {CB'D'} \right)} \right) = \dfrac{{a\sqrt 3 }}{3}\).

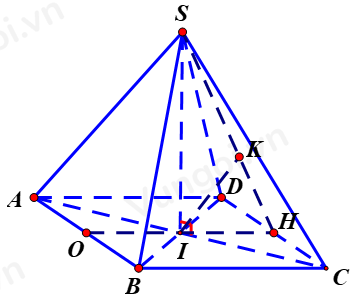
Gọi \({\rm{I }} = AC \cap BD.\)

\(AB = 2a \Rightarrow AI = a\sqrt 2 \)

\( \Rightarrow SI = \sqrt {S{A^2} - A{I^2}}  = \sqrt {{{(a\sqrt S )}^2} - {{(a\sqrt 2 )}^2}}  = a\sqrt 3 \)

Do \(AB//CD \Rightarrow d(AB;SCD) = d(;SCD) = 2d(;SCD)\)

Kẻ \(IH \bot CD;IK \bot SH = d(A;SCD) = IK\)

\(\dfrac{1}{{I{K^2}}} = \dfrac{1}{{S{I^2}}} + \dfrac{1}{{I{H^2}}} \Rightarrow IN = \dfrac{{a\sqrt 3 }}{2}\)

\( \Rightarrow d(AB;SCD) = a\sqrt 3 \)