Câu hỏi:
2 năm trước
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có đáy \(ABCD\) là hình vuông cạnh \(a\sqrt 2 \), \(AA' = 2a\). Tính khoảng cách giữa đường thẳng \(BD\) và mặt phẳng \(\left( {CB'D'} \right)\).
Trả lời bởi giáo viên
Đáp án đúng: b
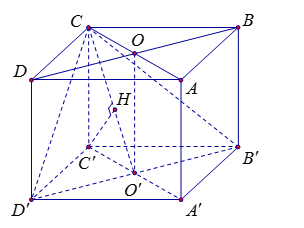
Gọi \(O,\,\)\(O'\) lần lượt là tâm của hai mặt đáy. Khi đó tứ giác \(COO'C'\)là hình bình hành và \(C'O' = \dfrac{{AC}}{2} = a\)
Do \(BD\;{\rm{//}}\;B'D'\)$ \Rightarrow BD\;{\rm{//}}\;\left( {CB'D'} \right)$ nên \(d\left( {BD;\left( {CB'D'} \right)} \right) = d\left( {O;\left( {CB'D'} \right)} \right) = d\left( {C';\left( {CB'D'} \right)} \right)\).
Ta có : \(\left\{ \begin{array}{l}B'D' \bot A'C'\\B'D' \bot CC'\end{array} \right. \Rightarrow B'D' \bot \left( {COO'C'} \right)\)\( \Rightarrow \left( {CB'D'} \right) \bot \left( {COO'C'} \right)\)
Lại có \(\left( {CB'D'} \right) \cap \left( {COO'C'} \right) = CO'\).
Trong \(\Delta CC'O'\) hạ \(C'H \bot CO' \Rightarrow C'H \bot \left( {CB'D'} \right)\)\( \Rightarrow d\left( {BD;\,CD'} \right) = C'H\)
Khi đó : \(\dfrac{1}{{C'{H^2}}} = \dfrac{1}{{C{{C'}^2}}} + \dfrac{1}{{C'{{O'}^2}}} = \dfrac{1}{{{{\left( {2a} \right)}^2}}} + \dfrac{1}{{{a^2}}} = \dfrac{5}{{4{a^2}}}\)\( \Rightarrow C'H = \dfrac{{2\sqrt 5 a}}{5}\).
Hướng dẫn giải:
Khoảng cách giữa đường thẳng và mặt phẳng song song bằng khoảng cách từ một điểm thuộc đường thẳng này đến mặt phẳng kia.
