Câu hỏi:
3 năm trước
Cho tứ diện $ABCD$ có $AC = a,{\rm{ }}BD = 3a$. Gọi $M{,^{}}N$ lần lượt là trung điểm của $AD$ và $BC$. Biết $AC$ vuông góc với $BD$. Tính $MN$.
Trả lời bởi giáo viên
Đáp án đúng: b
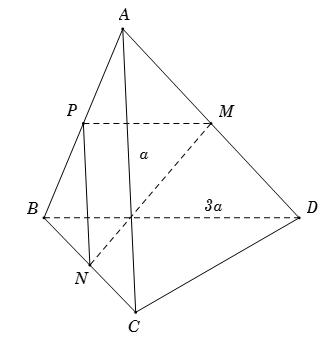
Gọi \(P\) là trung điểm của \(AB\) \( \Rightarrow PN,PM\) lần lượt là đường trung bình của tam giác \(\Delta ABC\) và \(\Delta ABD\). Suy ra \(\left\{ \begin{array}{l}PN = \dfrac{1}{2}AC = \dfrac{a}{2}\\PM = \dfrac{1}{2}BD = \dfrac{{3a}}{2}\end{array} \right..\)
Ta có \(AC \bot BD \Rightarrow PN \bot PM\) hay tam giác \(\Delta PMN\) vuông tại \(P\)
Do đó \(MN = \sqrt {P{N^2} + P{M^2}} = \sqrt {\dfrac{{{a^2}}}{4} + \dfrac{{9{a^2}}}{4}} = \dfrac{{a\sqrt {10} }}{2}.\)
Hướng dẫn giải:
Xét tính chất của tam giác \(MNP\) rồi suy ra độ dài \(MN\).