Cho tứ diện đều $ABCD$, $M$ là trung điểm của cạnh $BC$. Khi đó $\cos \left( {AB,DM} \right)$ bằng :

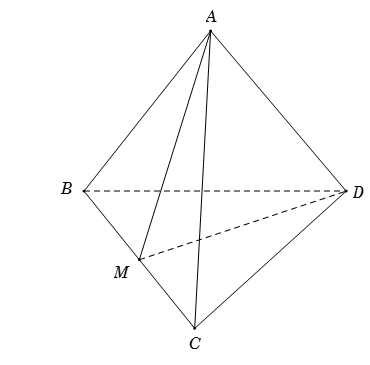
Giả sử cạnh của tứ diện là \(a\).

Tam giác \(BCD\) đều \( \Rightarrow DM = \dfrac{{a\sqrt 3 }}{2}\).

Tam giác \(ABC\) đều \( \Rightarrow AM = \dfrac{{a\sqrt 3 }}{2}\).

Ta có: $\cos \left( {\overrightarrow {AB} ,\overrightarrow {DM} } \right) = \dfrac{{\overrightarrow {AB} .\overrightarrow {DM} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {DM} } \right|}} = \dfrac{{\overrightarrow {AB} .\overrightarrow {DM} }}{{a.\dfrac{{a\sqrt 3 }}{2}}}$

Mặt khác: $\overrightarrow {AB} .\overrightarrow {DM}  = \overrightarrow {AB} \left( {\overrightarrow {AM}  - \overrightarrow {AD} } \right) = \overrightarrow {AB} .\overrightarrow {AM}  - \overrightarrow {AB} .\overrightarrow {AD} $

$\begin{array}{l} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AM} } \right|.\cos \left( {\overrightarrow {AB} .\overrightarrow {AM} } \right) - \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AD} } \right|.\cos \left( {\overrightarrow {AB} .\overrightarrow {AD} } \right)\\ = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AM} } \right|.\cos 30^\circ  - \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AD} } \right|.\cos 60^\circ \\ = a.\dfrac{{a\sqrt 3 }}{2}.\dfrac{{\sqrt 3 }}{2} - a.a.\dfrac{1}{2} = \dfrac{{3{a^2}}}{4} - \dfrac{{{a^2}}}{2} = \dfrac{{{a^2}}}{4}\end{array}$

$ \Rightarrow \cos \left( {\overrightarrow {AB} ,\overrightarrow {DM} } \right) = \dfrac{{\sqrt 3 }}{6} > 0 $ $\Rightarrow \left( {\overrightarrow {AB} ,\overrightarrow {DM} } \right) = \left( {AB,DM} \right) $ $\Rightarrow \cos \left( {AB,DM} \right) = \dfrac{{\sqrt 3 }}{6}$.