Câu hỏi:
2 năm trước
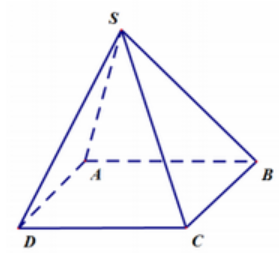
Cho tứ diện$ABCD$ có $AB = AC = AD$ và \(\widehat {BAC} = \widehat {BAD} = {60^0}\). Gọi $I$ và $J$ lần lượt là trung điểm của $AB$ và $CD$. Hãy xác định góc giữa cặp vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {IJ} \)?
Trả lời bởi giáo viên
Đáp án đúng: b
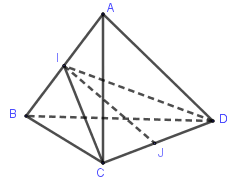
Xét tam giác\(ICD\) có \(J\) là trung điểm đoạn \(CD\).
Ta có: \(\overrightarrow {IJ} = \dfrac{1}{2}\left( {\overrightarrow {IC} + \overrightarrow {ID} } \right)\)
Vì tam giác \(ABC\) có \(AB = AC\) và \(\widehat {BAC} = 60^\circ \)
Nên tam giác \(ABC\)đều. Suy ra: \(CI \bot AB\)
Tương tự ta có tam giác \(ABD\) đều nên \(DI \bot AB\).
Xét \(\overrightarrow {IJ} .\overrightarrow {AB} = \dfrac{1}{2}\left( {\overrightarrow {IC} + \overrightarrow {ID} } \right).\overrightarrow {AB} = \dfrac{1}{2}\overrightarrow {IC} .\overrightarrow {AB} + \dfrac{1}{2}\overrightarrow {ID} .\overrightarrow {AB} = \overrightarrow 0 \).
Suy ra \(\overrightarrow {IJ} \bot \overrightarrow {AB} \). Hay góc giữa cặp vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {IJ} \) bằng \({90^0}\).
Hướng dẫn giải:
- Biểu diễn véc tơ \(\overrightarrow {IJ} \) qua hai véc tơ \(\overrightarrow {IC} ,\overrightarrow {ID} \).
- Sử dụng công thức tích vô hướng để tính góc giưa hai véc tơ.
