Câu hỏi:
2 năm trước
Cho hình lập phương \(ABCD.{A_1}{B_1}{C_1}{D_1}\) có cạnh $a$. Gọi $M$ là trung điểm $AD$. Giá trị \(\overrightarrow {{B_1}M} .\overrightarrow {B{D_1}} \) là:
Trả lời bởi giáo viên
Đáp án đúng: a
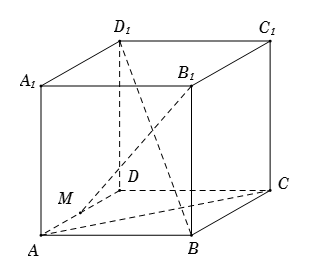
Ta có $\overrightarrow {{B_1}M} .\overrightarrow {B{D_1}} = \left( {\overrightarrow {{B_1}B} + \overrightarrow {BA} + \overrightarrow {AM} } \right)\left( {\overrightarrow {BA} + \overrightarrow {AD} + \overrightarrow {D{D_1}} } \right)$
\( = \underbrace {\overrightarrow {B{B_1}} .\overrightarrow {BA} }_{ = 0} + \underbrace {\overrightarrow {B{B_1}} .\overrightarrow {AD} }_{ = 0} + \overrightarrow {{B_1}B} .\overrightarrow {D{D_1}} + {\overrightarrow {BA} ^2} + \underbrace {\overrightarrow {BA} .\overrightarrow {AD} }_{ = 0}\) \( + \underbrace {\overrightarrow {BA} .\overrightarrow {D{D_1}} }_{ = 0}\)\( + \underbrace {\overrightarrow {AM} .\overrightarrow {BA} }_{ = 0} + \overrightarrow {AM} .\overrightarrow {AD} + \underbrace {\overrightarrow {AM} .\overrightarrow {D{D_1}} }_{ = 0}\)
$ = \overrightarrow {{B_1}B} .\overrightarrow {D{D_1}} + {\overrightarrow {BA} ^2} + \overrightarrow {AM} .\overrightarrow {AD} $$ = - {a^2} + {a^2} + \dfrac{{{a^2}}}{2} = \dfrac{{{a^2}}}{2}$.
Hướng dẫn giải:
Biểu diễn các véc tơ \(\overrightarrow {{B_1}M} ,\overrightarrow {B{D_1}} \) qua các véc tơ không đồng phẳng có phương là các cạnh của hình lập phương rồi tính tích vô hướng.
