Câu hỏi:
2 năm trước
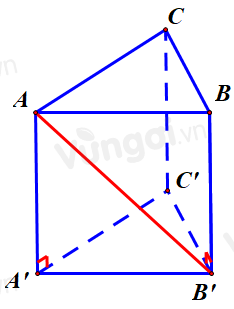
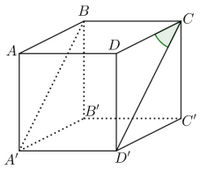
Trong không gian cho hai tam giác đều $ABC$ và $ABC'$ có chung cạnh $AB$ và nằm trong hai mặt phẳng khác nhau. Gọi $M,{\rm{ }}N,{\rm{ }}P,{\rm{ }}Q$ lần lượt là trung điểm của các cạnh $AC,{\rm{ }}CB,{\rm{ }}BC'$ và $C'A$ . Tứ giác $MNPQ$ là hình gì?
Trả lời bởi giáo viên
Đáp án đúng: b
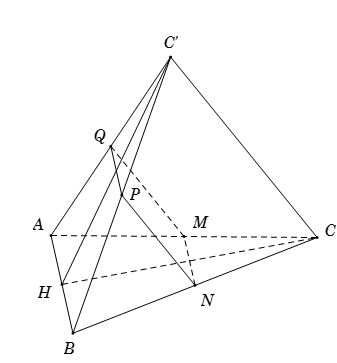
Vì $M,{\rm{ }}N,{\rm{ }}P,{\rm{ }}Q$ lần lượt là trung điểm của các cạnh $AC,{\rm{ }}CB,{\rm{ }}BC'$ và $C'A$
\( \Rightarrow \left\{ \begin{array}{l}PQ = MN = \dfrac{1}{2}AB\\PQ//AB//MN\end{array} \right.\)\( \Rightarrow \) \(MNPQ\) là hình bình hành.
Gọi \(H\) là trung điểm của \(AB\). Vì hai tam giác $ABC$ và $ABC'$ đều nên \(\left\{ \begin{array}{l}CH \bot AB\\C'H \bot AB\end{array} \right..\)
Suy ra \(AB \bot \left( {CHC'} \right)\). Do đó \(AB \bot CC'\).
Ta có \(\left\{ \begin{array}{l}PQ{\rm{//}}AB\\PN{\rm{//}}CC'\\AB \bot CC'\end{array} \right. \Rightarrow PQ \bot PN\) .
Vậy tứ giác $MNPQ$là hình chữ nhật.
Hướng dẫn giải:
Dựng hình, nhận xét tính chất của tứ giác dựa vào các mối quan hệ song song, vuông góc của các đường thẳng.
