Cho hình vuông \(ABCD\) tâm \(I\). Gọi \(M,N\) lần lượt là trung điểm của \(AD,DC.\) Phép tịnh tiến theo vecto nào sau đây biến \(\Delta AMI\) thành \(\Delta MDN?\)
Trả lời bởi giáo viên
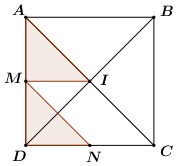
Ta có: \(IN\) là đường trung bình của tam giác \(ACD \Rightarrow IN = \dfrac{1}{2}AD = AM\).
\( \Rightarrow \overrightarrow {AM} = \overrightarrow {IN} \Rightarrow {T_{\overrightarrow {AM} }}\left( I \right) = N\).
Dễ thấy \(\overrightarrow {AM} = \overrightarrow {MD} \Rightarrow {T_{\overrightarrow {AM} }}\left( M \right) = D\) và hiển nhiên \({T_{\overrightarrow {AM} }}\left( A \right) = M\).
Vậy \({T_{\overrightarrow {AM} }}\left( {\Delta AMI} \right) = \Delta MDN\).
Hướng dẫn giải:
Phép tịnh tiến biến tam giác này thành tam giác kia là phép tịnh tiến biến mỗi đỉnh của tam giác này thành mỗi đỉnh tương ứng của tam giác kia.

