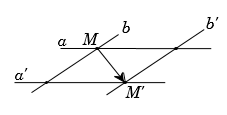
Cho bốn đường thẳng \(a,{\rm{ }}b,{\rm{ }}a',{\rm{ }}b'\) trong đó $a\parallel a'$, \(b\parallel b'\) và \(a\) cắt \(b\). Có bao nhiêu phép tịnh tiến biến \(a\) thành \(a'\) và \(b\) thành \(b'\)?

Trong hệ trục tọa độ \(Oxy\), cho \(\overrightarrow v \left( {3;3} \right)\) và đường tròn \(\left( C \right):\,\,{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\). Tìm phương trình đường tròn \(\left( {C'} \right)\) là ảnh của \(\left( C \right)\) qua phép tịnh tiến \({T_{\overrightarrow v }}.\)

Trong mặt phẳng với hệ tọa độ Oxy. Phép dời hình \(\left\{ \begin{array}{l}x' = x - 3\\y' = y + 1\end{array} \right.\) biến parabol \(\left( P \right):\,\,y = {x^2} + 1\) thành parabol \(\left( {P'} \right)\) có phương trình là:

Trong mặt phẳng Oxy cho đường thẳng d có phương trình x + 2y – 1 = 0 và vectơ \(\overrightarrow v \left( {2;m} \right)\). Để phép tịnh tiến theo \(\overrightarrow v \) biến đường thẳng d thành chính nó, ta phải chọn m là số:

Cho hình vuông \(ABCD\) tâm \(I\). Gọi \(M,N\) lần lượt là trung điểm của \(AD,DC.\) Phép tịnh tiến theo vecto nào sau đây biến \(\Delta AMI\) thành \(\Delta MDN?\)

Trong mặt phẳng tọa độ \(Oxy\), cho \(\Delta :\,\,x - 2y - 1 = 0\) và \(\overrightarrow u \left( {4;3} \right)\). Gọi \(d\) là đường thẳng sao cho \({T_{\overrightarrow u }}\) biến \(d\) thành đường thẳng \(\Delta \). Phương trình đường thẳng \(d\) là:

Trong mặt phẳng \(Oxy\), cho đường thẳng \(\Delta :\,2x - 3y - 5 = 0\). Ảnh của đường \(\Delta \) qua phép tịnh tiến theo vectơ \(\overrightarrow u  = \left( { - 1;2} \right)\) là đường thẳng nào?

Trong mặt phẳng tọa độ \(Oxy\), viết phương trình đường thẳng \(\Delta '\) là ảnh của đường thẳng \(\Delta :x + 2y - 1 = 0\) qua phép tịnh tiến theo véctơ \(\overrightarrow v  = \left( {1; - 1} \right)\).