Phép tịnh tiến

Biểu thức tọa độ của phép ${T_{\overrightarrow v }}$ là $\left\{ \begin{array}{l}x = x' + 2\\y = y' + 1\end{array} \right.$ thay vào $\left( P \right)$ ta được

$y' + 1 = {\left( {x' + 2} \right)^2} \Leftrightarrow y' = x{'^2} + 4x' + 3.$

Trên $d,{\rm{ }}d'$ lần lượt lấy $A,{\rm{ }}A'$ bất kì.

Khi đó, $d'$ là ảnh của $d$ qua phép tịnh tiến vectơ $\overrightarrow {AA'} .$

Vậy có vô số phép tịnh tiến biến $d$ thành $d'$ thỏa mãn $d$ song song $d'.$

Ta có $\left\{ \begin{array}{l}{T_{\vec u}}\left( M \right) = {M_1} \Leftrightarrow \overrightarrow {M{M_1}}  = \vec u\\{T_{\vec v}}\left( {{M_1}} \right) = {M_2} \Leftrightarrow \overrightarrow {{M_1}{M_2}}  = \vec v\end{array} \right.$$\Rightarrow \vec u + \vec v = \overrightarrow {M{M_1}}  + \overrightarrow {{M_1}{M_2}}  = \overrightarrow {M{M_2}}$

Đẳng thức $\overrightarrow {M{M_2}}  = \vec u + \vec v$ chứng tỏ phép tịnh tiến ${T_{\vec u + \vec v}}$ biến $M$ thành ${M_2}.$

Giả sử $M\left( {x;y} \right)$ là điểm có ảnh là điểm $A$ qua phép tịnh tiến theo vectơ $\vec v = \left( {1;2} \right)$$\Rightarrow \overrightarrow {MA}  = \left( {2 - x;5 - y} \right).$

Ta có ${T_{\overrightarrow v }}\left( M \right) = A \Leftrightarrow \overrightarrow {MA}  = \vec v$ $\Rightarrow \left\{ \begin{array}{l}2 - x = 1\\5 - y = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 3\end{array} \right.$

Có đúng một phép tịnh tiến. Tịnh tiến theo vectơ–không.

Đẳng thức $\overrightarrow {MM'}  = 2\overrightarrow {PQ}$ chứng tỏ phép tịnh tiến ${T_{2\overrightarrow {PQ} }}$ biến $M$ thành $M'.$

Thực hiện phép tịnh tiến theo phương của trục tung về phía dưới $4$ đơn vị, tức là thực hiện phép tịnh tiến theo vectơ $\overrightarrow u  = \left( {0; - 4} \right)$. Do đó đường thẳng $\Delta$ biến thành đường thẳng $\Delta '$ có phương trình: $y + 4 =  - 4x + 3 \Leftrightarrow y =  - 4x - 1$.

Đường tròn $\left( C \right)$ có tâm $I\left( {0;1} \right),$ bán kính $R = 1.$

Gọi $I'\left( {x;y} \right)$ là ảnh của $I\left( {0;1} \right)$ qua phép tịnh tiến vectơ $\vec v = \left( { - 3; - 2} \right)$.

Ta có $\overrightarrow {II'}  = \vec v \Leftrightarrow \left\{ \begin{array}{l}x - 0 =  - 3\\y - 1 =  - 2\end{array} \right.$$\Leftrightarrow \left\{ \begin{array}{l}x =  - 3\\y =  - 1\end{array} \right. \Rightarrow I'\left( { - 3; - 1} \right)$

Vì phép tịnh tiến bảo toàn khoảng cách nên $R' = R = 1.$

Vậy ảnh của đường tròn $\left( C \right)$ qua phép ${T_{\overrightarrow v }}$ là đường tròn $\left( {C'} \right)$ có tâm $I'\left( { - 3; - 1} \right),$ bán kính $T$ nên có phương  trình $\left( {C'} \right):{\left( {x + 3} \right)^2} + {\left( {y + 1} \right)^2} = 1.$

Từ giả thiết suy ra $d$ là ảnh của $\Delta$ qua phép tịnh tiến theo vectơ $\vec a = \vec u + \vec v$.

Ta có $\vec a = \vec u + \vec v = \left( {2;3} \right)$.

Biểu thức tọa độ của phép ${T_{\overrightarrow a }}$ là $\left\{ \begin{array}{l}x = x' - 2\\y = y' - 3\end{array} \right.$ thay vào $\Delta$ ta được$y' - 3 =  - 3\left( {x' - 2} \right) + 2$

$\Leftrightarrow \,y' =  - 3x' + 11$.

Đường tròn $\left( {{C_1}} \right)$ có tâm ${I_1}\left( {1; - 2} \right)$. Đường tròn $\left( {{C_2}} \right)$ có tâm ${I_2}\left( { - 3;4} \right)$.

Vì ${T_{\overrightarrow u }}\left[ {\left( {{C_1}} \right)} \right] = \left( {{C_2}} \right) \Rightarrow {T_{\overrightarrow u }}\left( {{I_1}} \right) = \left( {{I_2}} \right)$ $\Leftrightarrow \overrightarrow {{I_1}{I_2}}  = \overrightarrow u  \Rightarrow \overrightarrow u \left( { - 4;6} \right)$

Từ giả thiết suy ra $\left( {C'} \right)$ là ảnh của $\left( C \right)$ qua phép tịnh tiến theo $\vec a = \vec u + \vec v$.

Ta có $\vec a = \vec u + \vec v = \left( {2; - 3} \right)$.

Biểu thức tọa độ của phép ${T_{\overrightarrow a }}$ là $\left\{ \begin{array}{l}x = x' - 2\\y = y' + 3\end{array} \right.$ thay vào $\left( C \right)$ ta được

${\left( {x' - 2} \right)^2} + {\left( {y' + 3} \right)^2} + 4\left( {x - 2} \right) - 6\left( {y' + 3} \right) - 5 = 0$ $\Leftrightarrow x{'^2} + y{'^2} - 18 = 0$

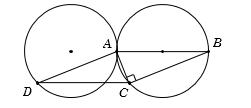
Ta có $\widehat {ACB} = {90^o}$ nên $C$ di động trên đường tròn đường kính $AB.$

Do $ABCD$ là hình bình hành nên ta có $\overrightarrow {CD}  = \overrightarrow {BA}$. Đẳng thức này chứng tỏ phép tịnh tiến theo vectơ $\overrightarrow {BA}$ biến điểm $C$ thành điểm $D$.

Vậy quỹ tích điểm $D$ là ảnh của đường tròn đường kính $AB$ qua phép tịnh tiến ${T_{\overrightarrow {BA} }}$.

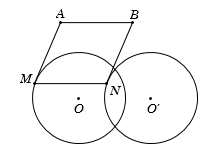
Do $MABN$ là hình bình hành nên ta có $\overrightarrow {MN}  = \overrightarrow {AB}$. Đẳng thức này chứng tỏ phép tịnh tiến theo vectơ $\overrightarrow {AB}$ biến điểm $M$ thành điểm $N$.

Mà $M$ thuộc $\left( {O,R} \right)$, suy ra $N$ thuộc đường tròn $\left( {O'} \right)$ là ảnh của $\left( O \right)$ qua phép tịnh tiến ${T_{\overrightarrow {AB} }}.$

Bước 1:

 Đường tròn $\left( C \right):\,\,{\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} = 4$ có tâm $I\left( {1; - 3} \right)$ và bán kính $R = 2$.

Bước 2:

Gọi $I' = {T_{\overrightarrow i }}\left( I \right) \Rightarrow \left\{ \begin{array}{l}{x_{I'}} = 1 + 1 = 2\\{y_{I'}} =  - 3 + 0 =  - 3\end{array} \right. \Rightarrow I'\left( {2; - 3} \right)$.

Bước 3:

Gọi $\left( {C'} \right) = {T_{\overrightarrow i }}\left( C \right) \Rightarrow \left( {C'} \right)$ là đường tròn có tâm $I'\left( {2; - 3} \right)$ và bán kính $R = 2$.

Vậy phương trình đường tròn $\left( {C'} \right):\,\,{\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} = 4$.

Ta có: $\left\{ \begin{array}{l}x = x' + 3\\y = y' - 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x' = x - 3\\y' = y + 5\end{array} \right. \Rightarrow \overrightarrow u  = \left( { - 3;5} \right)$

Mọi phép tịnh tiến theo véc tơ có giá song song hoặc trùng với đường thẳng $d$ đều biến $d$ thành chính nó

Vậy có vô số phép tịnh tiến như trên.

Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó.

Do đó không xảy ra trường hợp hai đường thẳng cắt nhau.

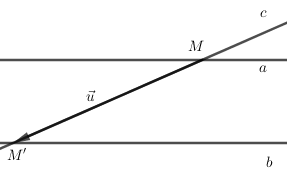
Phép tịnh tiến biến đường thẳng $c$ thành chính nó và đường thẳng $c$ cắt cả hai đường thẳng $a,b$ nên véc tơ tịnh tiến là véc tơ có giá song song hoặc trùng với $c$.

Từ hình vẽ ta thấy phép tịnh tiến theo véc tơ $\overrightarrow {MM'}$ biến $a$ thành $b$ và biến $c$ thành chính nó.

Có duy nhất một véc tơ thỏa mãn bài toán.

Cách 1:

Ta có: $y = \sin x = \sin \left( {x + k2\pi } \right) \Rightarrow \left\{ \begin{array}{l}x' = x + k2\pi \\y' = y\end{array} \right. \Rightarrow \overrightarrow u  = \left( {k2\pi ;0} \right)$

Do $k \in Z$ nên có vô số véc tơ $\overrightarrow u$ như trên.

Cách 2: Gọi vectơ tịnh tiến là $\overrightarrow v = \left( {a;b} \right)$. Ta có:

$\left\{ \begin{array}{l} x' = x + a\\ y' = y + b \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x = x' - a\\ y = y' - b \end{array} \right.$

Do $y = \sin x$ nên $y' - b = \sin \left( {x' - a} \right)$ $\Leftrightarrow y' = \sin \left( {x' - a} \right) + b$. Để $\overrightarrow v$ biến đồ thị thành chính nó thì $y' = \sin x'$ $\forall x'$ $\Leftrightarrow \sin x' = \sin \left( {x' - a} \right) + b$ $\forall x'$.

Với $x = 0 \Rightarrow 0 = - \sin a + b \Leftrightarrow \sin a = b$.

Với $x = \pi \Rightarrow 0 = \sin a + b \Leftrightarrow \sin a = - b$.

Với $x = \dfrac{\pi }{2} \Rightarrow 1 = \cos a + b \Leftrightarrow \cos a = 1 - b$.

Từ đó, ta có: $b = 0;a = k2\pi$

Gọi $B'(x;y)$ ta có:

$\overrightarrow {BB'}  = \overrightarrow {AA'}  \Leftrightarrow \left\{ \begin{array}{l}x - 2 = 2 - 3\\y - 5 = 5 - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 8\end{array} \right.$