Câu hỏi:
2 năm trước
Cho hình lăng trụ \(ABC.A'B'C'\). Gọi \(M,N\) lần lượt là trung điểm của \(BB',CC'\) và đường thẳng \(\Delta \) là giao tuyến của hai mặt phẳng \(\left( {AMN} \right)\) và \(\left( {A'B'C'} \right)\). Khẳng định nào sau đây đúng?
Trả lời bởi giáo viên
Đáp án đúng: c
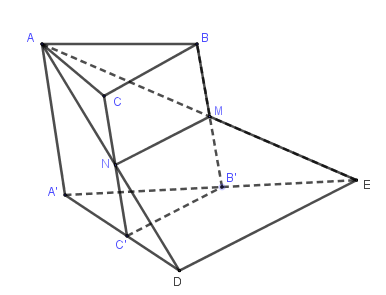
Gọi \(D = AN \cap A'C' \Rightarrow D \in \left( {AMN} \right) \cap \left( {A'B'C'} \right)\) và \(E = AM \cap A'B' \Rightarrow E \in \left( {AMN} \right) \cap \left( {A'B'C'} \right)\).
Khi đó \(DE = \left( {AMN} \right) \cap \left( {A'B'C'} \right) = \Delta \).
Lại có: \(\left\{ \begin{array}{l}\left( {AMN} \right) \cap \left( {MNC'B'} \right) = MN\\\left( {A'B'C'} \right) \cap \left( {MNC'B'} \right) = B'C'\\\left( {AMN} \right) \cap \left( {A'B'C'} \right) = DE\\MN//B'C'\end{array} \right. \Rightarrow MN//B'C'//DE\) (định lý ba giao tuyến)
Do đó \(DE//B'C'//BC\).
Hướng dẫn giải:
Xác định giao tuyến \(\Delta \) và xét tính đúng sai của từng đáp án.
Câu hỏi khác
- Bài tập đường thẳng song song với mặt phẳng toán 11 có lời giải
- Bài tập các bài toán tìm giao điểm của đường thẳng và mặt phẳng toán 11 có lời giải
- Bài tập thiết diện của hình chóp toán 11 có lời giải
- Bài tập hai đường thẳng song song toán 11 có lời giải
- Bài tập đại cương về đường thẳng và mặt phẳng toán 11 có lời giải
