Câu hỏi:
2 năm trước
Cho hình hộp \(ABCD.A'B'C'D'\), mặt phẳng \(\left( \alpha \right)\) qua \(AB\) và trung điểm \(M\) của \(CC'\) thì cắt hình hộp theo thiết diện là hình gì?
Trả lời bởi giáo viên
Đáp án đúng: c
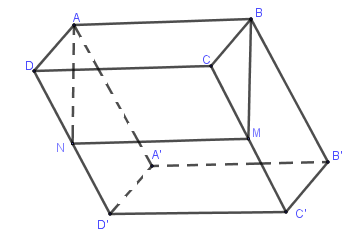
Ta sử dụng tính chất: Nếu một mặt phẳng cắt một trong hai mặt phẳng song song thì nó sẽ cắt mặt phẳng còn lại và giao tuyến của chúng song song.
Ta có:
\(\left. \begin{array}{l}\left( {ADD'A'} \right)//\left( {BCC'B'} \right)\\\left( {ABM} \right) \cap \left( {BCC'B'} \right) = BM\end{array} \right\} \Rightarrow \left( {ABM} \right) \cap \left( {ADD'A'} \right) = AN//BM\) với \(N \in DD'\).
Do đó tứ giác \(ABMN\) là hình thang.
Lại có:
\(\left. \begin{array}{l}\left( {ABB'A'} \right)//\left( {DCC'D'} \right)\\\left( {ABMN} \right) \cap \left( {ABB'A'} \right) = AB\\\left( {ABMN} \right) \cap \left( {DCC'D'} \right) = MN\end{array} \right\} \Rightarrow AB//MN\)
Do đó tứ giác \(ABMN\) là hình bình hành.
Hướng dẫn giải:
- Xác định thiết diện của hình hộp khi cắt bởi mặt phẳng \(\left( \alpha \right)\).
- Sử dụng các tính chất song song của đường thẳng, mặt phẳng để tìm hình dạng của thiết diện.
Câu hỏi khác
- Bài tập đường thẳng song song với mặt phẳng toán 11 có lời giải
- Bài tập các bài toán tìm giao điểm của đường thẳng và mặt phẳng toán 11 có lời giải
- Bài tập thiết diện của hình chóp toán 11 có lời giải
- Bài tập hai đường thẳng song song toán 11 có lời giải
- Bài tập đại cương về đường thẳng và mặt phẳng toán 11 có lời giải
