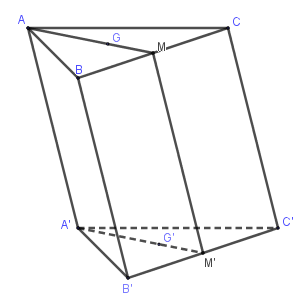
Cho hình lăng trụ \(ABC.A'B'C'\). Gọi \(M,M'\) lần lượt là trung điểm của \(BC\) và \(B'C'\), \(G,G'\) lần lượt là trọng tâm của các tam giác \(\Delta ABC,\Delta A'B'C'\). Bốn điểm nào sau đây đồng phẳng?

Cho lăng trụ đứng \(ABC.A'B'C'\). Mệnh đề nào sau đây sai?

Cho hình hộp $ABCD.A'B'C'D'$. Khẳng định nào sau đây sai?

Cho hình hộp $ABCD.A'B'C'D'$. Mặt phẳng $\left( {AB'D'} \right)$ song song với mặt phẳng nào trong các mặt phẳng sau đây?

Cho hình hộp \(ABCD.A'B'C'D'\). Gọi \(M\) là trung điểm của \(AB\), mặt phẳng \(\left( {MA'C'} \right)\) cắt hình hộp  \(ABCD.A'B'C'D'\). Gọi \(M\) là trung điểm của \(AB\), mặt phẳng \(\left( {MA'C'} \right)\) cắt hình hộp \(ABCD.A'B'C'D'\) theo thiết diện là hình gì?

Cho hình bình hành \(ABCD\). Vẽ các tia \(Ax,By,Cz,Dt\) song song, cùng hướng nhau và không nằm trong \(mp\left( {ABCD} \right)\). Mặt phẳng \(\left( \alpha  \right)\) cắt \(Ax,By,Cz,Dt\) lần lượt tại \(A',B',C',D'\), gọi \(O,O'\) lần lượt là tâm hình bình hành và giao điểm của hai đường thẳng \(A'C'\) với \(B'D'\). Khẳng định nào sau đây sai?

Số mặt chéo của hình hộp \(ABCD.A'B'C'D'\) là:

Cho hình hộp \(ABCD.A'B'C'D'\), mặt phẳng \(\left( \alpha  \right)\) qua \(AB\) và trung điểm \(M\) của \(CC'\) thì cắt hình hộp theo thiết diện là hình gì?