Câu hỏi:
2 năm trước
Cho hình hộp \(ABCD.A'B'C'D'\). Gọi \(I\) là trung điểm của \(AB\). Mặt phẳng \(\left( {IB'D'} \right)\) cắt hình hộp theo thiết diện là hình gì?
Trả lời bởi giáo viên
Đáp án đúng: b
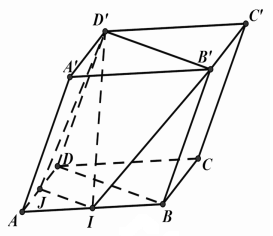
Ta có:
\(\left. \begin{array}{l}\left( {IB'D'} \right) \cap \left( {A'B'C'D'} \right) = B'D'\\\left( {A'B'C'D'} \right)//\left( {ABCD} \right)\end{array} \right\} \Rightarrow \left( {IB'D'} \right) \cap \left( {ABCD} \right) = JI//B'D'\) với \(J \in AD\)
Mà \(BD//B'D'\) nên \(JI//BD \Rightarrow J\) là trung điểm của \(AD\).
Vậy thiết diện là hình thang \(JIB'D'\).
Hướng dẫn giải:
- Xác định thiết diện của hình hộp: Sử dụng tính chất: “Nếu một mặt phẳng cắt một trong hai mặt phẳng song song thì nó cắt mặt phẳng còn lại và hai giao tuyến song song với nhau”.
- Sử dụng các tính chất song song để tìm hình dạng của thiết diện.
Câu hỏi khác
- Bài tập đường thẳng song song với mặt phẳng toán 11 có lời giải
- Bài tập các bài toán tìm giao điểm của đường thẳng và mặt phẳng toán 11 có lời giải
- Bài tập thiết diện của hình chóp toán 11 có lời giải
- Bài tập hai đường thẳng song song toán 11 có lời giải
- Bài tập đại cương về đường thẳng và mặt phẳng toán 11 có lời giải
