Câu hỏi:
2 năm trước
Cho bốn đường thẳng \(a,{\rm{ }}b,{\rm{ }}a',{\rm{ }}b'\) trong đó \(a\parallel a'\), \(b\parallel b'\) và \(a\) cắt \(b.\) Có bao nhiêu phép đối xứng tâm biến các đường thẳng \(a\) và \(b\) lần lượt thành các đường thẳng \(a'\) và \(b'?\)
Trả lời bởi giáo viên
Đáp án đúng: b
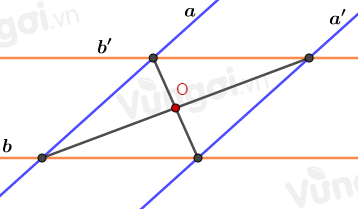
Đó là phép đối xứng qua tâm hình bình hành tạo thành bởi bốn đường thẳng đã cho.
Hướng dẫn giải:
Tìm tâm đối xứng và kết luận.

