Phép đối xứng tâm

Biểu thức tọa độ của phép đối xứng tâm $I\left( {a;b} \right)$ là $\left\{ \begin{array}{l}x' = 2a - x = 2 - x\\y' = 2b - y =  - y\end{array} \right.$$\Rightarrow \left\{ \begin{array}{l}x = 2 - x'\\y =  - y'\end{array} \right.$.

Thay vào $\left( E \right)$ ta được $\dfrac{{{{\left( {2 - x'} \right)}^2}}}{4} + \dfrac{{{{\left( { - y'} \right)}^2}}}{1} = 1$ $\Leftrightarrow \dfrac{{{{\left( {x' - 2} \right)}^2}}}{4} + \dfrac{{{{\left( { - y'} \right)}^2}}}{1} = 1$

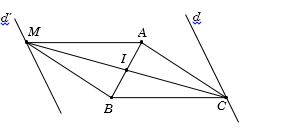
$M$ là ảnh của $C$ qua phép đối xứng tâm $I$ với $I$ là trung điểm $AB$.

Mà $C$ di động trên đường thẳng $d$ nên quỹ tích điểm $M$ là ảnh của đường thẳng $d$ qua phép đối xứng tâm $I.$

Từ giả thiết suy ra $DN = \dfrac{2}{3}DO$, mà $O$ là trung điểm $AC$$\Rightarrow$ $N$ là trọng tâm $\Delta ACD$.

Mà $AN$ cắt $CD$ tại $P$ $\Rightarrow$ $P$ là trung điểm $CD$.

Tương tự, ta có: $Q$ là trung điểm $AB$.

Do $AQ\parallel PC$ và $AQ = PC$ $\Rightarrow$ $AQCP$ là hình bình hành $\Rightarrow$ $O$ là trung điểm của $PQ$ $\Rightarrow$ $P$ và $Q$ đối xứng qua $O$.

Do $MO = NO = \dfrac{1}{6}BD$ $\Rightarrow$ $O$ là trung điểm $MN$ $\Rightarrow$ $M$ và $N$ đối xứng qua $O$.

Chứng minh tương tự $\Rightarrow$ $M$ là trọng tâm tam giác $ABC.$

Tam giác $ABC$ không phải là tam giác đều nên không đủ kết luận $M$ là tâm đường tròn ngoại tiếp tam giác $ABC$.

Lấy $A\left( {0;1} \right) \in d$, $B\left( {0; - 4} \right) \in d'$.

Vậy trung điểm $I$ của đoạn $AB$ là tâm đối xứng biến $d$ thành $d'$$\Rightarrow I\left( {\dfrac{{0 + 0}}{2};\dfrac{{1 + \left( { - 4} \right)}}{2}} \right) \Leftrightarrow I\left( {0;\dfrac{{ - 3}}{2}} \right)$.

Phép đối xứng biến đường thẳng thành đường thẳng song song với nó

+ Gọi đường thẳng $d'$ có ảnh là $d \Rightarrow d'\parallel d$.

$\Rightarrow d'$ có dạng: $x - y + c = 0$

+ Chọn điểm $A\left( {0;4} \right) \in d$.

+ Phép đối xứng tâm $I$ biến điểm $A$ thuộc $d$ thành $A'$ thuộc $d'$ $\Rightarrow I$ là trung điểm của $AA'$.

$\Leftrightarrow \left\{ \begin{array}{l}{x_I} = \dfrac{{{x_A} + {x_{A'}}}}{2}\\{y_I} = \dfrac{{{y_A} + {y_{A'}}}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_{A'}} = 2{x_I} - {x_A}\\{y_{A'}} = 2{y_I} - {y_A}\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l}{x_{A'}} = 8\\{y_{A'}} =  - 2\end{array} \right. \Rightarrow A'\left( {8; - 2} \right)$.

Vì $A' \in d'$, thay điểm $A'$ vào $d'$ ta có: $8 - \left( { - 2} \right) + c = 0 \Leftrightarrow c =  - 10$.

Vậy phương trình đường thẳng $d':\,\,x - y - 10 = 0$.

Từ hình vẽ ta thấy ảnh của $d$ trong phép đối xứng tâm $O\left( {0;0} \right)$ là đường thẳng $d':x =  - 2$.

Để phép đối xứng tâm $I$ biến $d$thành chính nó thì điểm $I$phải thuộc $\left( d \right):2x - y + 1 = 0$

Thay lần lượt từng đáp án vào $d$ ta thấy có đáp án D: $\left( {0;1} \right)$thỏa mãn.

Đường thẳng $\left( {d'} \right):x =  - 2$  là ảnh qua phép đối xứng tâm $O$của đường thẳng $\left( d \right):x = 2$.

Xét đáp án A: Hình chữ nhật có tâm đối xứng là giao điểm của 2 đường chéo.

Xét đáp án B: Tam giác đều không có tâm đối xứng.

Xét đáp án C: Lục giác đều có tâm đối xứng là giao của các đường chéo.

Xét đáp án D: Hình thoi có tâm đối xứng là giao của 2 đường chéo.

Hình 1 vừa có trục đối xứng và tâm đối xứng

Hình 2 và hình 3 có trục đối xứng nhưng không có tâm đối xứng

Hình 4 có tâm đối xứng nhưng không có trục đối xứng

Hình chữ nhật có tâm đối xứng là giao điểm hai đường chéo.

Hình tròn có tâm đối xứng là tâm hình tròn.

Hình tam giác đều không có tâm đối xứng.

Hình bình hành có tâm đối xứng là giao điểm hai đường chéo.

Bước 1:

Ảnh của $A$ qua phép đối xứng tâm $O\left( {0;0} \right)$ là $A'$.

Bước 2:

Ta có $\left\{ \begin{array}{l}{x_{A'}} = 2.0 - 1 =  - 1\\{y_{A'}} = 2.0 - \left( { - 3} \right) = 3\end{array} \right. \Rightarrow A'\left( { - 1;3} \right)$.

Gọi $M'$  là điểm đối xứng với $M$ qua tâm $I \Rightarrow I$ là trung điểm của $MM'$ .

$\Rightarrow \left\{ \begin{array}{l}{x_{M'}} = 2{x_I} - {x_M} =  - 1\\{y_{M'}} = 2{y_I} - {y_M} = 5\end{array} \right. \Rightarrow M'\left( { - 1;5} \right)$

${D_I}\left( I \right) = I \Rightarrow$ Phép đối xứng tâm có đúng một điểm biến thành chính nó.

Điểm đó chính là tâm đối xứng.

Phép đối xứng tâm biến đường thẳng thành đường thẳng song song với nó.

Dựa vào các đáp án ta thấy chỉ có đường thẳng đáp án C song song với đường thẳng $d$ đã cho.

${D_I}\left( M \right) = M' \Rightarrow I$ là trung điểm của $MM' \Rightarrow \left\{ \begin{array}{l}x + x' = 2a\\y + y' = 2b\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x' = 2a - x\\y' = 2b - y\end{array} \right.$

Hình vuông có tâm đối xứng là giao điểm của hai đường chéo.

Hình tròn có tâm đối xứng là tâm của nó.

Hình thoi có tâm đối xứng là giao điểm của hai đường chéo.

Tam giác đều không có tâm đối xứng

Tâm đối xứng của đường thẳng là điểm bất kỳ nằm trên đường thẳng $a$.

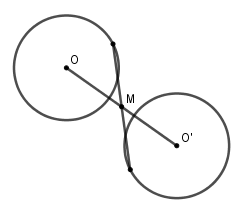
Hình gồm hai đường tròn phân biệt có cùng bán kính có tâm đối xứng duy nhất là trung điểm có đoạn thẳng nối tâm hai đường tròn đó

Đường tròn $\left( C \right)$  có tâm $K\left( {0;0} \right)$ và bán kính $R = 1$

Gọi ${D_I}\left( K \right) = K' \Rightarrow$ I  là trung điểm của  $KK' \Rightarrow K'\left( {2;0} \right)$

${D_I}\left( C \right) = \left( {C'} \right) \Rightarrow$ Đường tròn $\left( {C'} \right)$  có tâm $K'\left( {2;0} \right)$ và bán kính $R' = R = 1$

Vậy phương trình đường tròn $\left( {C'} \right)$ là: ${\left( {x - 2} \right)^2} + {y^2} = 1$