Câu hỏi:
2 năm trước
Trong mặt phẳng tọa độ \(Oxy\), cho \(A\left( {1;2} \right);\,\,B\left( {4;4} \right)\). Tìm điểm \(M\) thuộc \(Ox\) sao cho \(MA + MB\) nhỏ nhất?
Trả lời bởi giáo viên
Đáp án đúng: c
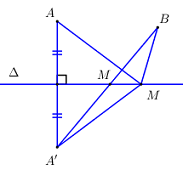
+ Dễ thấy \(A,B\) nằm cùng phía so với trục \(Ox\).
+ Gọi \(A' = \) Đ\(_{Ox}\left( A \right) \Rightarrow A'\left( {1; - 2} \right)\); khi đó ta có \(MA = MA'\).
\( \Rightarrow MA + MB = MA' + MB \ge A'B\).
Dấu "=" xảy ra \( \Leftrightarrow M,\,\,A',\,\,B\) thẳng hàng hay \(M = A'B \cap Ox\).
+ Phương trình \(A'B:\,\,\frac{{x - 1}}{{4 - 1}} = \frac{{y + 2}}{{4 + 2}} \Leftrightarrow 2\left( {x - 1} \right) = y + 2 \Leftrightarrow 2x - y - 4 = 0\).
+ Tọa độ của \(M\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}2x - y - 4 = 0\\y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 0\end{array} \right. \Rightarrow M\left( {2;0} \right)\).
Hướng dẫn giải:
Bài toán: Trong mặt phẳng cho hai điểm phân biệt \(A,\,B\) và không nằm trên đường thẳng \(\Delta \) cho trước. Tìm điểm \(M \in \Delta \) sao cho \(MA + MB\) nhỏ nhất.
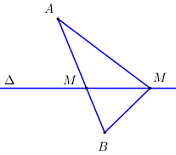
+ TH1: A và B nằm khác phía đối với \(\Delta \). Khi đó ta có \(MA + MB \ge AB\), dấu bằng xảy ra khi \(M,\,\,A,\,\,B\) thẳng hàng, tức \(M = AB \cap \Delta \)
+ TH2: A và B nằm cùng phía đối với \(\Delta \). Ta gọi \(A'\) là ảnh của \(A\) qua Đ\(_\Delta \). Khi đó \(\forall M \in \Delta :\,\,MA + MB = MA' + MB\).
Mà \(MA' + MB\) bé nhất khi \(M,\,\,A',\,\,B\) thẳng hàng hay \(M = A'B \cap \Delta \).
