Trong mặt phẳng $Oxy$ cho đường thẳng $d$ có phương trình \(x - y + 1 = 0\) và hai điểm\(A\left( {3;1} \right);B\left( {7;5} \right)\). Tìm điểm $M$ thuộc $d$ sao cho \(MA + MB\) nhỏ nhất ?

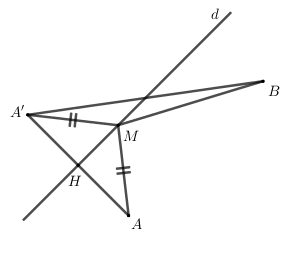
Ta dễ dàng kiểm tra được $A,B$ nằm cùng phía so với đường thẳng $d$.

Gọi $A'$  là điểm đối xứng với $A$ qua $d$ , ta có : \(MA = MA'\)

\( \Rightarrow MA + MB = MA' + MB \ge A'B\)

\( \Rightarrow MA + MB\) nhỏ nhất \( \Leftrightarrow M,A',B\) thẳng hàng hay \(M = A'B \cap d\).

Đường thẳng $AA'$  đi qua $A$ và vuông góc với $d$ nên có phương trình \(x + y - 4 = 0\,\,\left( {d'} \right)\).

Gọi \(H = d \cap d' \Rightarrow \) Tọa độ điểm $H$ là nghiệm của hệ

$\left\{ \begin{array}{l}x - y + 1 = 0\\x + y - 4 = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = \dfrac{3}{2}\\y = \dfrac{5}{2}\end{array} \right. \Rightarrow H\left( {\dfrac{3}{2};\dfrac{5}{2}} \right)$ là trung điểm của  \(AA' \Rightarrow \left\{ \begin{array}{l}{x_{A'}} = 2{x_H} - {x_A} = 0\\{y_{A'}} = 2{y_H} - {y_H} = 4\end{array} \right. \Rightarrow A'\left( {0;4} \right)\) 

\( \Rightarrow \) Phương trình đường thẳng $A'B$  là : \(\dfrac{{x - 0}}{{7 - 0}} = \dfrac{{y - 4}}{{5 - 4}} \Leftrightarrow \dfrac{x}{7} = y - 4 \Leftrightarrow x - 7y + 28 = 0\)

\( \Rightarrow MA + MB\) nhỏ nhất \( \Leftrightarrow M = A'B \cap d \Rightarrow \) Tọa độ điểm $M$ là nghiệm của hệ \(\left\{ \begin{array}{l}x - y + 1 = 0\\x - 7y + 28 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{7}{2}\\y = \dfrac{9}{2}\end{array} \right. \Rightarrow M\left( {\dfrac{7}{2};\dfrac{9}{2}} \right)\) .