Câu hỏi:
2 năm trước
Cho góc nhọn $xOy$ và điểm $A$ thuộc miền trong của góc đó, điểm $B$ thuộc cạnh $Ox$ ($B$ khác $O$). Tìm $C$ thuộc $Oy$ sao cho chu vi tam giác $ABC$ nhỏ nhất?
Trả lời bởi giáo viên
Đáp án đúng: d
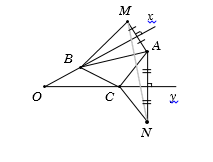
Gọi $M$ là điểm đối xứng với $A$ qua $Ox.$ Vì $B \in Ox$ nên suy ra $BA = BM.$
Gọi $N$ là điểm đối xứng với $A$ qua $Oy$. Vì $C \in Oy$ nên suy ra $CA = CN.$
Chu vi tam giác: ${P_{\Delta ABC}} = AB + BC + CA = BM + BC + CN.$ \(\left( * \right)\)
Theo bất đẳng thức tam giác mở rộng, ta có
$MB + BC \ge MC$ và $MC + CN \ge MN.$
Kết hợp với $\left( * \right)$, suy ra
${P_{\Delta ABC}} = \left( {MB + BC} \right) + CN \ge MC + CN \ge MN.$
Dấu xảy ra khi và chỉ khi $B,\,\,C,\,\,M,\,\,N$ thẳng hàng hay $C$ là giao điểm của $BM$ với trục $Oy$.
Hướng dẫn giải:
- Gọi $M$ là điểm đối xứng với $A$ qua $Ox.$
- Gọi $N$ là điểm đối xứng với $A$ qua $Oy$.
- Đánh giá GTNN của chu vi tam giác \(ABC\) và kết luận.
