Trong mặt phẳng tọa độ \(C'\left( {4;16} \right).\) cho điểm $M\left( {2;3} \right)$. Hỏi trong bốn điểm sau điểm nào là ảnh của \(M\) qua phép đối xứng đường thẳng $d:x - y = 0$?
Nhận xét: đường thẳng $d:x - y = 0 \Leftrightarrow d:y = x$ là đường phân giác của góc phần tư thứ nhất.
Biểu thức tọa độ qua phép đối xứng đường phân giác \(y = x\) là:
Gọi \(M'\left( {x';y'} \right) = \)${D_d}\left[ {M\left( {x;y} \right)} \right]$ thì \(\left\{ \begin{array}{l}x' = y\\y' = x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x' = 3\\y' = 2\end{array} \right..\)
Trong mặt phẳng tọa độ \(Oxy\), gọi $d$ là đường phân giác của góc phần tư thứ hai. Phép đối xứng trục ${D_d}$ biến điểm $P\left( {5; - 2} \right)$ thành điểm $P'$ có tọa độ là:
Đường phân giác của góc phần tư thứ hai có phương trình \(d:y = - x.\)
Biểu thức tọa độ qua phép đối xứng đường phân giác \(d:y = - x\) là:
Gọi \(P'\left( {x';y'} \right) = \)${D_d}\left[ {P\left( {x;y} \right)} \right]$ thì \(\left\{ \begin{array}{l}x' = - y\\y' = - x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x' = 2\\y' = - 5\end{array} \right..\)
Trong mặt phẳng tọa độ \(Oxy\) cho parabol $\left( P \right):y = {x^2} - 2x + 3.$ Phép đối xứng trục $Ox$ biến parabol $\left( P \right)$ thành parabol $\left( {P'} \right)$ có phương trình là:
Biểu thức tọa độ qua phép đối xứng trục \(Ox\) là $\left\{ \begin{array}{l}x = x'\\y = - y'\end{array} \right..$
Thay vào \(\left( P \right)\), ta được $ - y' = x{'^2} - 2x' + 3$ hay $y' = - x{'^2} + 2x' - 3.$
Tìm $m$ để \(\left( C \right):\,\,{x^2} + {y^2} + 4x + 2my + 8 = 0\) là ảnh của đường tròn \(\left( {C'} \right):\,\,{\left( {x - 10} \right)^2} + {\left( {y - 3} \right)^2} = 5\) qua phép đối xứng trục $d$, biết đường thẳng $d$ có phương trình \(x = 4.\)
Đường tròn \(\left( C \right)\) có tâm \(I\left( {3; - m} \right)\) là ảnh của tâm \(I'\left( {10;3} \right)\) của đườngtròn \(\left( {C'} \right)\) qua phép đối xứng trục $d$ .
$II'$ là đường thẳng đi qua $I'$ và vuông góc với d nên có phương trình $y = 3$.
Gọi $H$ là giao điểm của đường thẳng $x = 4$ và \(y = 3 \Rightarrow H\left( {4;3} \right)\) là trung điểm của \(II' \Rightarrow I'\left( { - 2;3} \right)\)
\( \Leftrightarrow m = - 3\)
Trong mặt phẳng tọa độ $Oxy$, phép đối xứng trục biến điểm $A\left( {2;1} \right)$ thành $A'\left( {2;5} \right)$ có trục đối xứng là:
Gọi ${D_a}\left( A \right) = A'$ $ \Rightarrow a$ là đường trung trực của đoạn thẳng $AA'.$
Gọi $H$ là trung điểm đoạn thẳng $AA' \Rightarrow H\left( {2;3} \right).$
Ta có $\overrightarrow {AA'} = \left( {0;4} \right) = 4.\left( {0;1} \right).$
Đường thẳng $a$ qua điểm $H$ và có một VTPT $\vec n = \overrightarrow {AA'} = \left( {0;4} \right)$ nên có phương trình $a:y = 3.$
Trong mặt phẳng tọa độ $Oxy$, nếu phép đối xứng trục biến điểm $M\left( {2;3} \right)$ thành $M'\left( {3;2} \right)$ thì nó biến điểm $C\left( {1; - 6} \right)$ thành điểm:
Gọi ${D_a}\left( M \right) = M'$ $ \Rightarrow a$ là đường trung trực của đoạn thẳng $MM'.$
Gọi $I$ là trung điểm đoạn thẳng $MM' \Rightarrow I\left( {\dfrac{5}{2};\dfrac{5}{2}} \right).$
Đường thẳng $a$ qua điểm $I$ và có một vtpt $\vec n = \overrightarrow {MM'} = \left( {1; - 1} \right)$ nên có phương trình $a:x - y = 0$ hay $a:y = x$ (đường phân giác góc phần tư thứ nhất).
Suy ra \(C'\left( { - 6;1} \right).\)
Mệnh đề nào sau đây là sai?
Trường hợp đường thẳng không song song hoặc không trùng với trục đối xứng thì ảnh của nó sẽ cắt đường thẳng đã cho (Hình vẽ).

Trong mặt phẳng tọa độ $Oxy$ cho đường thẳng \(\Delta \) có phương trình $5x + y - 3 = 0.$ Đường thẳng đối xứng của $\Delta $ qua trục tung có phương trình là:
Biểu thức tọa độ qua phép đối xứng trục tung là \(\left\{ \begin{array}{l}x' = - x\\y' = y\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = - x'\\y = y'\end{array} \right..\)
Thay vào $\Delta $, ta được $ - 5x' + y' - 3 = 0$ hay $5x' - y' + 3 = 0$.
Trong mặt phẳng tọa độ $Oxy$, gọi $a$ là đường phân giác của góc phần tư thứ nhất. Ta xét đường thẳng $\Delta :3x - 4y + 5 = 0.$ Phép đối xứng trục ${D_a}$ biến đường thẳng $\Delta $ thành đường thẳng $\Delta '$ có phương trình là:
Biểu thức tọa độ qua phép đối xứng ${D_a}$ là \(\left\{ \begin{array}{l}x' = y\\y' = x\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = y'\\y = x'\end{array} \right..\)
Thay vào $\Delta $, ta được $3y' - 4x' + 5 = 0.$ hay $4x' - 3y' - 5 = 0.$
Cho hai đường thẳng song song \(a\) và \(b\), một đường thẳng \(c\) vuông góc với chúng. Có bao nhiêu phép đối xứng trục biến mỗi đường thẳng đó thành chính nó?
Để biến đường thẳng \(c\) thành chính nó thì trục đối xứng có dạng trùng với \(c\) hoặc vuông góc với \(c.\)
TH1: Trục đối xứng trùng với \(c\) \( \Rightarrow \) trục đối xứng vuông góc với \(a\) và \(b\)
\( \Rightarrow \) trục đối xứng biến \(a\) và \(b\) thành chính nó. Do đó trường hợp này thỏa mãn.
TH2: Trục đối xứng vuông góc với \(c\), tức là trục đối xứng song song (hoặc trùng) với \(a\) và \(b\). Khi đó, trục đối xứng không thể biến \(a\) và \(b\) thành chính nó.
Vậy có duy nhất một phép đối xứng trục thỏa mãn bài toán
Cho hai đường thẳng song song \(a\) và \(b\), một đường thẳng \(c\) vuông góc với chúng. Có bao nhiêu phép đối xứng trục biến \(a\) thành \(b\) và \(c\) thành chính nó?
Để biến đường thẳng \(c\) thành chính nó thì trục đối xứng có dạng trùng với \(c\) hoặc vuông góc với \(c.\)
TH1: Trục đối xứng trùng với \(c\) \( \Rightarrow \)trục đối xứng vuông góc với \(a\) và \(b\)
\( \Rightarrow \) trục đối xứng biến \(a\) và \(b\) thành chính nó. Do đó trường hợp này không thỏa mãn.
TH2: Trục đối xứng vuông góc với \(c\), tức là trục đối xứng song song (hoặc trùng) với \(a\) và \(b\). Khi đó, để trục đối xứng biến \(a\) thành \(b\) thì trục đối xứng phải cách đều \(a\) và \(b\).
Do đó trường hợp này có 1 trục đối xứng thỏa mãn.
Ảnh $A'$ của $A\left( {4; - 3} \right)$ qua phép đối xứng trục $d$ với \(d:2x\; - y = 0\) có tọa độ là:
Gọi \(A'\) là ảnh của $A$ qua phép đối xứng trục $d.$ Gọi $d’$ là đường thẳng đi qua $A $ và vuông góc với $d,$ khi đó phương trình $d’$ có dạng: $x + 2y + c = 0.$
Vì \(A \in d'\) nên \(4 + 2\left( { - 3} \right) + c = 0 \Rightarrow c = 2\). Khi đó \(\left( {d'} \right):x + 2y + 2 = 0\)
Gọi \(H = d \cap d' \Rightarrow H\left( { - \dfrac{2}{5}; - \dfrac{4}{5}} \right) \Rightarrow \) $H $ là trung điểm của $AA’.$ Khi đó
\(\left\{ \begin{array}{l}{x_{A'}} = 2{x_H} - {x_A}\\{y_{A'}} = 2{y_H} - {y_A}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_{A'}} = 2.\left( { - \dfrac{2}{5}} \right) - 4 = - \dfrac{{24}}{5}\\{y_{A'}} = 2\left( { - \dfrac{4}{5}} \right) + 3 = \dfrac{7}{5}\end{array} \right. \Rightarrow A'\left( { - \dfrac{{24}}{5};\dfrac{7}{5}} \right)\)
Hình gồm $2$ đường tròn có tâm và bán kính khác nhau có bao nhiêu trục đối xứng?
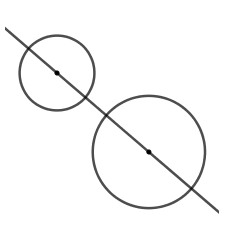
Hình gồm $2$ đường tròn có tâm và bán kính khác nhau có trục đối xứng duy nhất là đường thẳng nối tâm của $2$ đường tròn đó.
Trong mặt phẳng $Oxy$ cho tam giác $ABC$ với $A\left( {1;3} \right),B\left( {2; - 4} \right),C\left( {3; - 2} \right)$ và điểm $G$ và trọng tâm tam giác $ABC$. Ảnh $G'$ của $G$ qua phép đối xứng trục $Ox$ có tọa độ là
\(\left\{ \begin{array}{l}{x_G} = \dfrac{{{x_A} + {x_B} + {x_C}}}{3} = \dfrac{{1 + 2 + 3}}{3} = 2\\{y_G} = \dfrac{{{y_A} + {y_B} + {y_C}}}{3} = \dfrac{{3 - 4 - 2}}{3} = - 1\end{array} \right. \Rightarrow G\left( {2; - 1} \right) \Rightarrow G'\left( {2;1} \right)\)
Cho điểm $N\left( { - 2;3} \right)$. Khẳng định nào sau đây đúng
Điểm $M\left( { - 2; - 3} \right)$ là ảnh đối xứng của điểm $N$ qua phép đối xứng trục $Ox$.
Hình nào sau đây có nhiều trục đối xứng nhất ?
Hình thoi có $2$ trục đối xứng (hai đường chéo).
Hình vuông có $4$ trục đối xứng (hai đường chéo và hai đường thẳng đi qua trung điểm các cạnh đối).
Elip có $2$ trục đối xứng (hai trục của Elip)
Hình tròn có vô số trục đối xứng là các đường thẳng đi qua tâm (đường kính).
Trong mặt phẳng tọa độ \(Oxy\) cho đường tròn \(\left( C \right):{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 4\). Phép đối xứng trục \(Ox\) biến đường tròn \(\left( C \right)\) thành đường tròn \(\left( {C'} \right)\) có phương trình là:
Đường tròn \(\left( C \right)\) có tâm \(I\left( {1; - 2} \right)\) và bán kính \(R = 2.\)
Ta có \(I\left( {1; - 2} \right) \Rightarrow I'\left( {1;2} \right)\) đối xứng với \(I\) qua \(Ox\) và \(R = 2 \Rightarrow R' = R = 2.\)
Do đó \(\left( {C'} \right)\) có phương trình \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 4.\)
Số phát biểu đúng trong các phát biểu sau:
(1) Phép tịnh tiến và phép đối xứng trục đều biến đường thẳng thành đường thẳng song song, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đương tròn thành đường tròn có cùng bán kính.
(2) Tứ giác $ABCD$ là hình thang cân đáy \(AD//BC\). Gọi $M,N$ lần lượt là trung điểm của hai cạnh bên $AB$ và $CD$. Khi đó, đường thẳng $MN$ là trục đối xứng của $ABCD$.
(3) Cho đường thẳng $d$ có phương trình \(y = - x\). Ảnh của đường tròn \(\left( C \right):\,\,{\left( {x - 5} \right)^2} + {\left( {y - 3} \right)^2} = 7\) qua phép đối xứng trục $d$ là \(\left( {C'} \right):\,\,{\left( {x - 5} \right)^2} + {\left( {y + 3} \right)^2} = 7\)
(4) Ảnh của đường phân giác ứng với góc phần tư thứ $(I)$ qua phép đối xứng trục $Oy$ là đường thẳng $d$ có phương trình \(y = - x\)
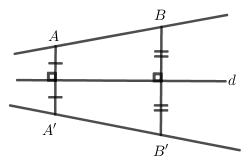
Dựa vào hình vẽ trên ta thấy $2$ đường thẳng đối xứng qua đường thẳng $d$ không song song \( \Rightarrow \) (1) sai.
Xét (2): \(M,N\) là trung điểm của hai cạnh bên \(AB,CD\) nên \(MN\) là đường trung bình của hình thang chứ không phải trục đối xứng. Trục đối xứng của hình thang cân là đường thẳng đi qua trung điểm hai đáy nên (2) sai.
Xét (3): Đường tròn \(\left( C \right)\) có tâm \(I\left( {5;3} \right)\) và bán kính \(R = \sqrt 7 \), đường tròn \(\left( {C'} \right)\) có tâm \(I'\left( {5; - 3} \right)\), bán kính \(R' = \sqrt 7 \)
Gọi $H$ là trung điểm của \(II' \Rightarrow H\left( {5;0} \right) \notin \left( {y = - x} \right) \Rightarrow \left( 3 \right)\) sai.
Xét (4): Đường phân giác ứng với góc phần tư thứ $(I) $ có phương trình \(y = x\) có ảnh qua phép đối xứng trục $Oy$ là đường phân giác của góc phần tư thứ $(II)$ có phương trình \(y = - x \Rightarrow \left( 4 \right)\) đúng.
Vậy chỉ có $1$ phát biểu đúng.
Trong mặt phẳng $Oxy$ cho parabol \(\left( P \right):y=4{x^2} - 7x + 3\). Phép đối xứng trục $Oy$ biến $\left( P \right)$ thành $\left( {P'} \right)$ có phương trình
Phép đối xứng trục $Oy$ có: \(\left\{ \begin{array}{l}x = - x'\\y = y'\end{array} \right.\)
Thay vào phương trình $\left( P \right)$ ta có: \(y = 4{\left( { - x} \right)^2} - 7\left( { - x} \right) + 3 = 4{x^2} + 7x + 3\)
Trong mặt phẳng tọa độ $Oxy$ cho đường tròn \(\left( {C'} \right):{x^2} + {y^2} - 10x - 2y + 23 = 0\) và đường thẳng $d:x-y + 2 = 0$, phương trình đường tròn $\left( {C'} \right)$ là ảnh của đường tròn $\left( C \right)$ qua phép đối xứng trục $d$ là
Đường tròn $\left( C \right)$ có tâm $I\left( {5;1} \right)$ bán kính \(R = \sqrt {25 + 1 - 23} = \sqrt 3 \).
Ảnh của $\left( C \right)$ qua phép đối xứng trục $d$ là đường tròn có tâm là ảnh của $I$ qua phép đối xứng trục $d$ và có bán kính bằng \(\sqrt 3 \).
Gọi $I'$ là ảnh của $I$ qua phép đối xứng trục $d$. Gọi $d'$ là đường thẳng đi qua $I$ và vuông góc với $d$ ta có phương trình $d'$ có dạng $x + y + c = 0$ .
\(I \in d' \Rightarrow 5 + 1 + c = 0 \Rightarrow c = - 6\) \( \Rightarrow \left( {d'} \right):x + y - 6 = 0\)
Gọi \(H = d \cap d' \Rightarrow H\left( {2;4} \right)\) là trung điểm của $II'$ , ta có \(\left\{ \begin{array}{l}{x_{I'}} = 2{x_H} - {x_I}\\{y_{I'}} = 2{y_H} - {y_I}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_{I'}} = 2.2 - 5 = - 1\\{y_{I'}} = 2.4 - 1 = 7\end{array} \right. \Rightarrow I'\left( { - 1;7} \right)\)
Vậy phương trình đường tròn $\left( {C'} \right)$ là \({\left( {x + 1} \right)^2} + {\left( {y - 7} \right)^2} = 3 \) \(\Leftrightarrow {x^2} + {y^2} + 2x - 14y + 47 = 0\)

