Trong mặt phẳng Oxy, cho hai đường tròn (C):(x−1)2+(y−2)2=4 và (C′):(x−3)2+y2=4. Viết phương trình trục đối xứng của (C) và (C′)
Đường tròn (C) có tâm I(1;2), đường tròn (C′) có tâm I′(3;0)
Gọi H là trung điểm của II′ ta có H(2;1)
Trục đối xứng của 2 đường tròn (C) và (C′) là đường thẳng đi qua H và nhận →II′=(2;−2)=2(1;−1) là 1 VTPT ⇒ Trục đối xứng của 2 đường tròn (C) và (C′) có phương trình 1(x−2)−1(y−1)=0 ⇔x−2−y+1=0 ⇔y=x−1
Khẳng định nào sau đây sai ?
Phép đối xứng trục không bảo toàn hướng của vector.
Trong mặt phẳng tọa độ Oxy cho đường thẳng d:x+y−2=0. Ảnh của đường thẳng d qua phép đối xứng trục Ox có phương trình là:
Trục Ox có phương trình y=0.
Tọa độ giao điểm A của d và Ox thỏa mãn hệ {x+y−2=0y=0⇒A(2;0).
Vì A∈Ox nên qua phép đối xứng trục Ox biến thành chính nó, tức A′≡A(2;0).
Chọn điểm B(1;1)∈d⇒B′(1;−1) là ảnh của B qua phép đối xứng trục Ox.
Vậy đường thẳng d′ là ảnh của d qua phép đối xứng trục Ox đi qua hai điểm A′(2;0) và B′(1;−1) nên có phương trình x−y−2=0.
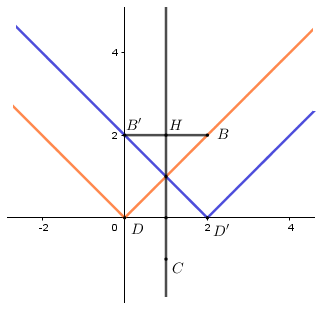
Cho hàm số (C):y=|x|. Giả sử (C′) đối xứng với (C) qua đường thẳng x=1. Khi đó, hàm số có đồ thị (C′) có dạng :
(C):y=|x|=[xkhix≥0(d1)−xkhix<0(d2)
d1∩(x=1)=A(1;1)
Lấy B(2;2)∈d1⇒ đường thẳng đi qua B và vuông góc với đường thẳng x=1 có phương trình y=2.
Gọi H là giao điểm của đường thẳng x=1 và y=2⇒H(1;2)
Gọi B′ là điểm đối xứng với B qua đường thẳng x=1⇒H là trung điểm của BB′⇒B′(0;2)
⇒ Phương trình đường thẳng AB′ là x−10−1=y−12−1⇔−x+1=y−1⇔x+y=2
⇒x+y=2 là đường thẳng đối xứng với đường thẳng y=x qua đường thẳng x=1.
d2∩(x=1)=C(1;−1)
Lấy D(0;0)∈d2⇒ Đường thẳng đi qua D và vuông góc với đường thẳng x=1 có phương trình y=0.
Gọi K là giao điểm của đường thẳng x=1 và y=0⇒K(1;0)
Gọi D′ là điểm đối xứng với D qua đường thẳng x=1⇒K là trung điểm của DD′⇒D′(2;0)
⇒ Phương trình đường thẳng CD′ là : x−12−1=y+10+1⇔x−1=y+1⇔x−y=2
⇒x−y=2 là đường thẳng đối xứng với đường thẳng y=−x qua đường thẳng x=1
⇒(C′):[x+y=2x−y=2⇒[y=−x+2y=x−2⇔y=|x−2|
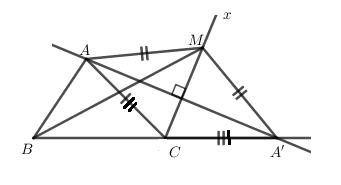
Trên tia phân giác ngoài Cx của góc C của tam giác ABC lấy điểm M không trùng với C . Tìm mệnh đề đúng nhất ?
Lấy A′ đối xứng với A qua Cx ta có :
{MA=MA′CA=CA′ ⇒MA+MB=MA′+MB >A′B=CA′+CB=CA+CB
Với mọi tứ giác ABCD, kí hiệu S là diện tích của tứ giác ABCD. Chọn mệnh đề đúng ?
Gọi d là đường trung trực của cạnh đoạn thẳng AC.
Lấy D′ đối xứng với D qua đường thẳng d⇒AD=CD′;AD′=CD
⇒S=SABCD′=SABD′+SBCD′
Ta có :
SABD′=12AB.AD′.sin^BAD′≤12AB.AD′=12AB.CDSBCD′=12BC.CD′.sin^BCD′≤12BC.CD′=12BC.AD⇒S≤12(AB.CD+BC.AD)
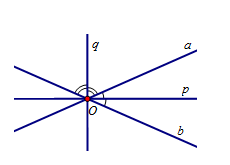
Cho hai đường thẳng a và b cắt nhau tại điểm O. Nhận định nào sau đây là đúng?
Gọi p và q là phân giác của các góc tạo bởi hai đường thẳng a và b . Ta thấy ngay có hai phép đối xứng trục biến a thành b là các phép đối xứng trục Dp và Dq.
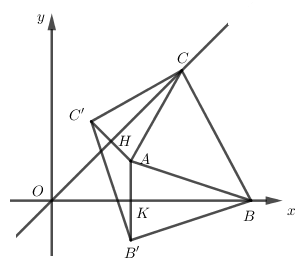
Cho điểm A(2;1). Tìm điểm B trên trục hoành và điểm C trên đường phân giác của góc phần tư thứ nhất để chu vi tam giác ABC nhỏ nhất.
Gọi B′,C′ lần lượt là điểm đối xứng với A qua trục Ox và đường thẳng y=x ta có : AB=BB′,AC=CC′
Dễ thấy B′(2;−1)
AC′ là đường thẳng đi qua A và vuông góc với đường thẳng y=x nên có phương trình x+y−3=0.
Gọi H là giao điểm của đường thẳng y=x và x+y−3=0⇒H(32;32) là trung điểm của AC′⇒C′(1;2)
Chu vi tam giác ABC là :
C=AB+BC+CA=B′B+BC+CC′≥B′C′⇒Cmin
Phương trình B'C':
\dfrac{{x - 2}}{{1 - 2}} = \dfrac{{y + 1}}{{2 + 1}} \Leftrightarrow - x + 2 = \dfrac{{y + 1}}{3} \Leftrightarrow - 3x + 6 = y + 1 \Leftrightarrow 3x + y - 5 = 0
\Rightarrow B\left( {\dfrac{5}{3};0} \right),C\left( {\dfrac{5}{4};\dfrac{5}{4}} \right)
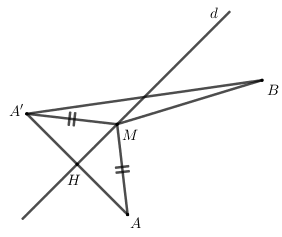
Cho x,y thỏa mãn x - 2y + 2 = 0. Tìm giá trị nhỏ nhất của biểu thức T = \sqrt {{{\left( {x - 3} \right)}^2} + {{\left( {y - 5} \right)}^2}} + \sqrt {{{\left( {x - 5} \right)}^2} + {{\left( {y - 7} \right)}^2}}
Gọi M\left( {x;y} \right) thỏa mãn x - 2y + 2 = 0 \Rightarrow M thuộc đường thẳng x - 2y + 2 = 0\,\,\left( d \right).
Gọi A\left( {3;5} \right);B\left( {5;7} \right) \Rightarrow T = MA + MB
Ta cần tìm điểm M \in d sao cho MA + MB nhỏ nhất.
Dễ thấy A,B nằm cùng phía so với đường thẳng d.
Gọi A' là điểm đối xứng với A qua d ta có: MA = MA'
\Rightarrow MA + MB = MA' + MB \ge A'B
\Rightarrow MA + MB nhỏ nhất \Leftrightarrow M,A',B thẳng hàng hay M = A'B \cap d.
Đường thẳng AA' đi qua A và vuông góc với d nên có phương trình 2x + y - 11 = 0\,\,\left( {d'} \right).
Gọi H = d \cap d' \Rightarrow Tọa độ điểm H là nghiệm của hệ:
\left\{ \begin{array}{l}x - 2y + 2 = 0\\2x + y - 11 = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 4\\y = 3\end{array} \right. \Rightarrow H\left( {4;3} \right) là trung điểm của AA' \Rightarrow \left\{ \begin{array}{l}{x_{A'}} = 2{x_H} - {x_A} = 5\\{y_{A'}} = 2{y_H} - {y_H} = 1\end{array} \right. \Rightarrow A'\left( {5;1} \right)
\Rightarrow Phương trình đường thẳng A'B là : x = 5.
\Rightarrow MA + MB nhỏ nhất \Leftrightarrow M = A'B \cap d \Rightarrow Tọa độ điểm M là nghiệm của hệ \left\{ \begin{array}{l}x - 2y + 2 = 0\\x = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5\\y = \dfrac{7}{2}\end{array} \right. \Rightarrow M\left( {5;\dfrac{7}{2}} \right) \Rightarrow {T_{\min }} = 6.
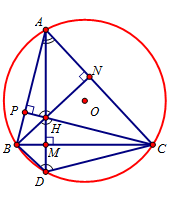
Cho hai điểm B và C cố định trên đường tròn \left( {O;R} \right). Điểm A thay đổi trên \left( {O;R} \right). Gọi H là trực tâm của \Delta ABC và D là điểm đối xứng của H qua đường thẳng BC . Mệnh đề nào sau đây là đúng?
Trong một tam giác, điểm đối xứng của trực tâm H qua một cạnh của nó thì nằm trên đường tròn ngoại tiếp tam giác đó. Đây là một kiến thức cơ bản. Tuy nhiên ta có thể chứng minh lại bài toán này như sau:
Kẻ các đường cao AM,BN,CP và gọi D là điểm đối xứng của H qua BC.
Ta có tứ giác ANHP là một tứ giác nội tiếp, suy ra: \widehat {PAN} + \widehat {PHN} = {180^o} hay \widehat {BAC} + \widehat {BHC} = {180^o}.
Mặt khác, có D là điểm đối xứng của H qua BC nên \widehat {BDC} = \widehat {BHC}.
Do đó: \widehat {BAC} + \widehat {BDC} = {180^o}.
Suy ra D nằm trên đường tròn \left( O \right) ngoại tiếp \Delta ABC.
Đường thẳng đối xứng với đường thẳng d:\left\{ \begin{array}{l}x = 1 + 2t\\y = - 2 + t\end{array} \right. qua đường thẳng \Delta :2{\rm{x}} + y + 6 = 0 có phương trình là
d:\,\,\left\{ \begin{array}{l}x = 1 + 2t\\y = - 2 + t\end{array} \right. \Rightarrow x - 2y - 5 = 0 \Rightarrow \overrightarrow {{n_1}} = \left( {1; - 2} \right).
Ta có: \Delta :\,\,\,2x + y + 6 = 0 \Rightarrow \overrightarrow {{n_2}} = \left( {2;1} \right).
Xét: \overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 1.2 + \left( { - 2} \right).1 = 0 \Rightarrow Đường thẳng d \bot \Delta .
Vậy đường thẳng đối xứng với d qua \Delta vẫn chính là d:\,\,x - 2y - 5 = 0.
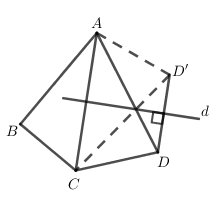
Cho đường tròn \left( {O;R} \right) đường kính AB. Điểm M nằm trên AB. Qua AB kẻ dây CD tạo với AB một góc {45^0}. Gọi D' là điểm đối xứng của D qua AB. Tính M{C^2} + MD{'^2} theo R?
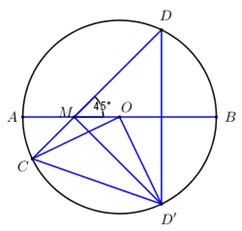
D' = Đ_{AB}\left( D \right) \Rightarrow AB là trung trực của DD' \Rightarrow MD = MD' và \angle DMB = \angle D'MB = {45^0}.
\Rightarrow \angle DMD' = {90^0} \Rightarrow \Delta MDD' vuông cân tại M.
\Rightarrow \angle MDD' = {45^0}.
Mà \angle MDD' = \dfrac{1}{2}\angle COD' (góc nội tiếp và góc ở tâm cùng chắn cung CD')
\Rightarrow \angle COD' = {90^0} \Rightarrow \Delta OCD' vuông cân tại O.
Do O\in AB là trung trực của DD'\Rightarrow OD=OD'=R\Rightarrow D'\in \left( O;R \right).
Áp dụng định lí Pytago trong tam giác vuông OCD' ta có : CD{{'}^{2}}=O{{C}^{2}}+OD{{'}^{2}}={{R}^{2}}+{{R}^{2}}=2{{R}^{2}}.
Ta có \angle DMD' = {90^0} (cmt) \Rightarrow \angle CMD' = {90^0} \Rightarrow \Delta CMD' vuông tại M.
Áp dụng định lí Pytago trong tam giác vuông CMD' ta có : M{C^2} + MD{'^2} = CD{'^2} = 2{R^2}.
Xem các chữ cái in hoa A, B, C, D, X, Y như những hình. Khẳng định nào sau đây đúng?
Khẳng định đúng là B.

