Câu hỏi:
2 năm trước
Cho hai điểm $B$ và $C$ cố định trên đường tròn $\left( {O;R} \right)$. Điểm $A$ thay đổi trên $\left( {O;R} \right)$. Gọi $H$ là trực tâm của $\Delta ABC$ và $D$ là điểm đối xứng của $H$ qua đường thẳng $BC$ . Mệnh đề nào sau đây là đúng?
Trả lời bởi giáo viên
Đáp án đúng: d
Trong một tam giác, điểm đối xứng của trực tâm $H$ qua một cạnh của nó thì nằm trên đường tròn ngoại tiếp tam giác đó. Đây là một kiến thức cơ bản. Tuy nhiên ta có thể chứng minh lại bài toán này như sau:
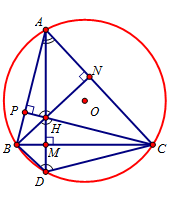
Kẻ các đường cao $AM,BN,CP$ và gọi $D$ là điểm đối xứng của $H$ qua $BC$.
Ta có tứ giác $ANHP$ là một tứ giác nội tiếp, suy ra: $\widehat {PAN} + \widehat {PHN} = {180^o}$ hay $\widehat {BAC} + \widehat {BHC} = {180^o}$.
Mặt khác, có $D$ là điểm đối xứng của $H$ qua $BC$ nên $\widehat {BDC} = \widehat {BHC}$.
Do đó: $\widehat {BAC} + \widehat {BDC} = {180^o}$.
Suy ra $D$ nằm trên đường tròn $\left( O \right)$ ngoại tiếp $\Delta ABC$.
Hướng dẫn giải:
Vẽ hình và dựa vào các kiến thức về tứ giác nội tiếp.
