Câu hỏi:
3 năm trước
Với mọi tứ giác $ABCD$, kí hiệu $S$ là diện tích của tứ giác $ABCD$. Chọn mệnh đề đúng ?
Trả lời bởi giáo viên
Đáp án đúng: b
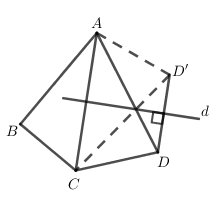
Gọi $d$ là đường trung trực của cạnh đoạn thẳng $AC$.
Lấy $D'$ đối xứng với $D$ qua đường thẳng \(d \Rightarrow AD = CD';AD' = CD\)
\( \Rightarrow S = {S_{ABCD'}} = {S_{ABD'}} + {S_{BCD'}}\)
Ta có :
\(\begin{array}{l}{S_{ABD'}} = \dfrac{1}{2}AB.AD'.\sin \widehat {BAD'} \le \dfrac{1}{2}AB.AD' = \dfrac{1}{2}AB.CD\\{S_{BCD'}} = \dfrac{1}{2}BC.CD'.\sin \widehat {BCD'} \le \dfrac{1}{2}BC.CD' = \dfrac{1}{2}BC.AD\\ \Rightarrow S \le \dfrac{1}{2}\left( {AB.CD + BC.AD} \right)\end{array}\)
Hướng dẫn giải:
Lấy $D'$ đối xứng với $D$ qua đường trung trực của $AC$

