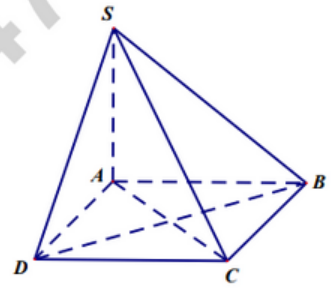
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật tâm $O.$ Đường thẳng \(SA\) cuông góc với mặt đáy \(\left( {ABCD} \right)\). Gọi $I$ là trung điểm của $SC.$ Khẳng định nào dưới đây là sai ?
Trả lời bởi giáo viên
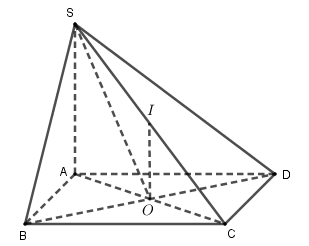
Vì $O,\,\,I$ lần lượt là trung điểm của $AC,\,\,SC$ suy ra $OI$ là đường trung bình của tam giác $SAC$$ \Rightarrow $$OI$//$SA$ mà $SA \bot \left( {ABCD} \right) \Rightarrow OI \bot \left( {ABCD} \right).$
Ta có $ABCD$ là hình chữ nhật $ \Rightarrow \,\,\,BC \bot AB$ mà $SA \bot BC$ suy ra $BC \bot SB.$
Tương tự, ta có được $\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\,\,\,\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right. \Rightarrow CD \bot SD.$
Nếu $\left( {SAC} \right)$ là mặt phẳng trung trực của $BD\,\, \Rightarrow \,BD \bot AC$: điều này không thể xảy ra vì $ABCD$ là hình chữ nhật.
Hướng dẫn giải:
Sử dụng định nghĩa đường thẳng vuông góc với mặt phẳng để xét tính đúng, sai của từng đáp án.