Câu hỏi:
2 năm trước
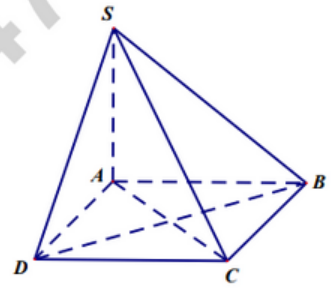
Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật và \(SA\) vuông góc với đáy. Khi đó số mặt bên của hình chóp là tam giác vuông bằng :
Trả lời bởi giáo viên
Đáp án đúng: a
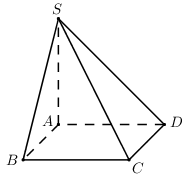
Ta có :
\(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB\)\( \Rightarrow \Delta SAB\) vuông tại \(A\).
\(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AD\)\( \Rightarrow \Delta SAD\) vuông tại \(A\).
Ta có \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right.\)
\( \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB\)
\( \Rightarrow \Delta SBC\) vuông tại \(B\).
\(\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right.\)\( \Rightarrow CD \bot \left( {SAD} \right) \Rightarrow CD \bot SD\)\( \Rightarrow \Delta SCD\) vuông tại \(D\).
Vậy cả bốn mặt của hình chóp đều là tam giác vuông.
Hướng dẫn giải:
Xét 4 mặt (SAB), (SAD), (SBC), (SCD).
Sử dụng định lí \(d \bot \left( P \right) \Rightarrow d \bot a\,\,\forall a \in \left( P \right)\).
