Câu hỏi:
2 năm trước
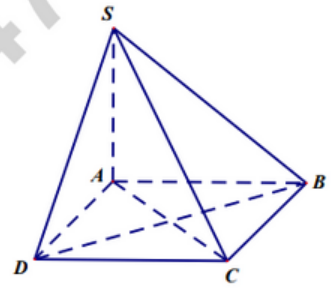
Cho hình chóp \(S.ABCD\) với đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\) , có \(AD = CD = a\), \(AB = 2a\). Cạnh bên \(SA\) vuông góc với đáy \(\left( {ABCD} \right)\), \(E\) là trung điểm của \(AB\). Chỉ ra mệnh đề sai trong các mệnh đề sau:
Trả lời bởi giáo viên
Đáp án đúng: d
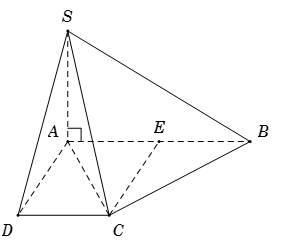
Từ giả thết suy ra \(ADCE\) là hình vuông \( \Rightarrow \left\{ \begin{array}{l}CE \bot AB\\CE = AD = a\end{array} \right..\)
Ta có \(\left\{ \begin{array}{l}CE \bot AB\\CE \bot SA{\rm{ }}\left( {{\rm{do }}SA \bot ABCD} \right)\end{array} \right. \Rightarrow CE \bot \left( {SAB} \right).\) Do đó A đúng.
Vì \(CE = AD = a \Rightarrow CE = \dfrac{1}{2}AB \Rightarrow \Delta ABC\) vuông tại \(C \Rightarrow CB \bot AB\). Kết hợp với \(CB \bot SA\) (do \(SA \bot \left( {ABCD} \right)\)) nên suy ra \(CB \bot \left( {SAC} \right).\) Do đó B đúng.
Ta có \(\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA{\rm{ }}\left( {{\rm{do }}SA \bot ABCD} \right)\end{array} \right. \Rightarrow CD \bot \left( {SAD} \right) \Rightarrow CD \bot SD.\) Do đó C đúng.
Dùng phương pháp loại trừ, suy ra D là đáp án sai.
Hướng dẫn giải:
Sử dụng các mối quan hệ hình học tính độ dài các đoạn thẳng, từ đó sử dụng định nghĩa, tính chất đường thẳng vuông góc mặt phẳng để nhận xét từng đáp án.
