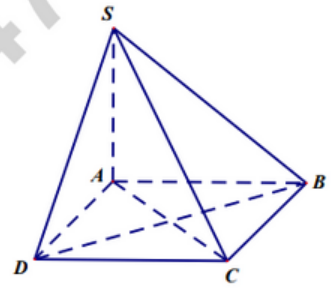
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, cạnh bên $SA$ vuông góc với mặt phẳng đáy. Gọi $AE,\,\,AF$ lần lượt là đường cao của tam giác $SAB$ và tam giác $SAD.$ Khẳng định nào dưới đây là đúng ?

Nếu \(a//(\alpha )\) và \(b//(\alpha )\) thì \(a \bot b\).

Nếu \(a \bot (\alpha )\) và \(b \bot (\alpha )\) thì \(a \bot b\).

Nếu \(b//(\alpha )\) và \(a \bot (\alpha )\) thì \(a \bot b\).

Nếu \(b/4(\alpha )\) và \(a \bot b\) thì \(a \bot (\alpha )\).

\(BD \bot (SAC)\).

\(CD \bot (SAD)\).

\(AC \bot (SBD)\).

\(BC \bot (SAB)\).

\(BC \bot \left( {SAB} \right)\).      

\(BC \bot \left( {SAJ} \right)\).       

\(BC \bot \left( {SAC} \right)\)       

\(BC \bot \left( {SAM} \right)\).

4

1

2

3

Nếu đường thẳng \(d \bot \left( \alpha  \right)\) thì \(d\) vuông góc với hai đường thẳng trong \(\left( \alpha  \right)\).

Nếu đường thẳng \(d\) vuông góc với hai đường thẳng nằm trong \(\left( \alpha  \right)\) thì \(d \bot \left( \alpha  \right)\).

Nếu đường thẳng \(d\) vuông góc với hai đường thẳng cắt nhau nằm trong \(\left( \alpha  \right)\) thì \(d\) vuông góc với bất kì đường thẳng nào nằm trong \(\left( \alpha  \right)\).

Nếu \(d \bot \left( \alpha  \right)\) và đường thẳng \(a\;{\rm{//}}\;\left( \alpha  \right)\) thì $d \bot a$.

Nếu \(a{\rm{//}}\left( P \right)\) và \(b \bot a\) thì \(b{\rm{//}}\left( P \right)\).

Nếu \(a{\rm{//}}\left( P \right)\) và \(b \bot \left( P \right)\) thì \(a \bot b\).

Nếu \(a{\rm{//}}\left( P \right)\) và \(b \bot a\) thì \(b \bot \left( P \right)\).

Nếu \(a \bot \left( P \right)\) và \(b \bot a\) thì \(b{\rm{//}}\left( P \right)\).

\(1\)

Vô số

\(3\)

\(2\)