Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông, cạnh bên \(SA\) vuông góc với mặt phẳng đáy. Đường thẳng \(SD\) tạo với mặt phẳng \(\left( {SAB} \right)\) một góc \(45^\circ \). Gọi \(I\) là trung điểm của cạnh \(CD\). Góc giữa hai đường thẳng \(BI\) và \(SD\) bằng (Số đo góc được làm tròn đến hàng đơn vị).
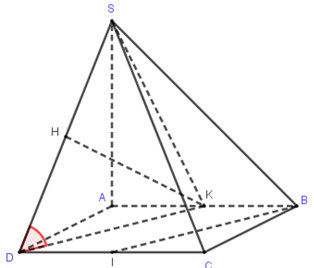
Giả sử hình vuông \(ABCD\) cạnh \(a\), \(\left( {\widehat {SD,\,\left( {SAB} \right)}} \right) = 45^\circ \)\( \Rightarrow SA = AD = a\)
Gọi \(K\) là trung điểm của \(AB\).
Vì \(KD\,{\rm{//}}\,BI\) nên góc giữa hai đường thẳng \(BI\) và \(SD\) bằng góc giữa hai đường thẳng \(KD\) và \(SD\) và là góc \(\widehat {SDK}\).
Ta có \(KD = SK = \dfrac{{a\sqrt 5 }}{2}\), \(SD = a\sqrt 2 \).
Gọi \(H\) là trung điểm của \(SD\). Ta có \(\cos \widehat {SDK} = \dfrac{{HD}}{{KD}} = \dfrac{{\dfrac{{a\sqrt 2 }}{2}}}{{\dfrac{{a\sqrt 5 }}{2}}} = \dfrac{{\sqrt {10} }}{5}\).
Vậy góc giữa hai đường thẳng \(BI\) và \(SD\) bằng \(51^\circ .\)
Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ có các cạnh $AB = 2,\,\,AD = 3;\,AA' = 4$. Góc giữa hai mặt phẳng $\left( {AB'D'} \right)$ và $\left( {A'C'D} \right)$ là $\alpha $. Tính giá trị gần đúng của góc $\alpha $?
Hai mặt phẳng $\left( {AB'D'} \right)$ và $\left( {A'C'D} \right)$ có giao tuyến là $EF$ như hình vẽ.
Hai tam giác \(\Delta A'C'D = \Delta D'AB'\) và \(EF\) là đường trung bình của hai tam giác nên từ $A'$ và $D'$ ta kẻ 2 đoạn vuông góc lên giao tuyến $EF$ sẽ là chung một điểm $H$ như hình vẽ.
Khi đó, góc giữa hai mặt phẳng cần tìm chính là góc giữa hai đường thẳng $A'H$ và $D'H$.
Tam giác $DEF$ lần lượt có $D'E = \dfrac{{D'B'}}{2} = \dfrac{{\sqrt {13} }}{2}$, $D'F = \dfrac{{D'A}}{2} = \dfrac{5}{2}$, $EF = \dfrac{{B'A}}{2} = \sqrt 5 $.
Theo hê rông ta có: ${S_{DEF}} = \dfrac{{\sqrt {61} }}{4}$. Suy ra $D'H = \dfrac{{2{S_{DEF}}}}{{EF}} = \dfrac{{\sqrt {305} }}{{10}}$.
Tam giác $D'A'H$ có: $\cos \widehat {A'HD'} = \dfrac{{H{{A'}^2} + H{{D'}^2} - A'{{D'}^2}}}{{2HA'.HD'}} = - \dfrac{{29}}{{61}}$.
Do đó $\widehat {A'HD'} \approx 118,4^\circ $ hay $\left( {\widehat {A'H,D'H}} \right) \approx 180^\circ - 118,4^\circ = 61,6^\circ $.
Cho hình chóp tam giác đều \(S.ABC\) có độ dài cạnh đáy bằng \(a\), cạnh bên bằng $a\sqrt 3 $. Gọi \(O\) là tâm của đáy \(ABC\), \({d_1}\) là khoảng cách từ \(A\) đến mặt phẳng \(\left( {SBC} \right)\) và \({d_2}\) là khoảng cách từ \(O\) đến mặt phẳng \(\left( {SBC} \right)\). Tính \(d = {d_1} + {d_2}\).
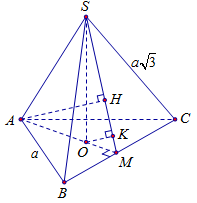
Do tam giác \(ABC\) đều tâm \(O\) suy ra \(AO \bot BC\) tại \(M\) là trung điểm của \(BC\).
Ta có:\(AM = \dfrac{{a\sqrt 3 }}{2},\,MO = \dfrac{1}{3}AM = \dfrac{{a\sqrt 3 }}{6},\,OA = \dfrac{2}{3}AM = \dfrac{{a\sqrt 3 }}{3}\).
Từ giả thiết hình chóp đều suy ra \(SO \bot \left( {ABC} \right)\), \(SO = \sqrt {S{A^2} - O{A^2}} = \sqrt {3{a^2} - \dfrac{{3{a^2}}}{9}} = \dfrac{{2a\sqrt 6 }}{3}\).
Dựng \(OK \bot SM,AH \bot SM \Rightarrow AH{\rm{//}}OK;\,\,\dfrac{{OK}}{{AH}} = \dfrac{{OM}}{{AM}} = \dfrac{1}{3}\).
Có \(\left\{ \begin{array}{l}BC \bot SO\\BC \bot AM\end{array} \right. \Rightarrow BC \bot \left( {SAM} \right) \Rightarrow BC \bot OK\).
Có \(\left\{ \begin{array}{l}OK \bot SM\\OK \bot BC\end{array} \right. \Rightarrow OK \bot \left( {SBC} \right),\,AH \bot \left( {SBC} \right)\,\,\left( {{\rm{ do } }AH{\rm{//}} OK} \right)\).
Từ đó có \({d_1} = d\left( {A,\left( {SBC} \right)} \right) = AH = 3OK;\,{d_2} = d\left( {O,\left( {SBC} \right)} \right) = OK\).
Trong tam giác vuông $OSM$ có đường cao \(OK\) nên:
\(\dfrac{1}{{O{K^2}}} = \dfrac{1}{{O{M^2}}} + \dfrac{1}{{S{O^2}}} = \dfrac{{36}}{{3{a^2}}} + \dfrac{9}{{24{a^2}}} = \dfrac{{99}}{{8{a^2}}} \Rightarrow OK = \dfrac{{2a\sqrt {22} }}{{33}}\).
Vậy \(d = {d_1} + {d_2} = 4OK = \dfrac{{8a\sqrt {22} }}{{33}}\).
Cho hình chóp \(S.ABCD\), đáy là hình thang vuông tại \(A\) và \(B\), biết \(AB = BC = a\), \(AD = 2a\), \(SA = a\sqrt 3 \) và \(SA \bot \left( {ABCD} \right)\). Gọi \(M\) và \(N\) lần lượt là trung điểm của \(SB\), \(SA\). Tính khoảng cách từ \(M\) đến \(\left( {NCD} \right)\) theo \(a\).
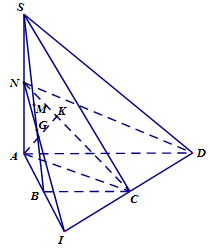
Gọi \(I\) là giao điểm của \(AB\) và \(CD\), vì \(AD = 2BC\) nên \(B\) là trung điểm của \(AI\).
Gọi \(G\) là giao điểm của \(SB\) và \(IN\), dễ thấy \(G\) là trọng tâm tam giác \(SAI\).
Do đó, \(SG = \dfrac{2}{3}SB = \dfrac{4}{3}SM \Rightarrow MG = \dfrac{1}{4}SG\), mà \(G \in \left( {NCD} \right)\) nên $d\left( {M;\,\left( {NCD} \right)} \right) = \dfrac{1}{4}d\left( {S;\,\left( {NCD} \right)} \right) = \dfrac{1}{4}d\left( {A;\,\left( {NCD} \right)} \right)$.
Lại có, \(CD \bot AC;\,CD \bot SA \Rightarrow CD \bot \left( {SAC} \right)\).
Gọi \(K\) là hình chiếu của \(A\) lên \(NC\) thì $d\left( {A;\,\left( {NCD} \right)} \right) = AK = \dfrac{{AN.AC}}{{\sqrt {A{N^2} + A{C^2}} }}\,\,\,\left( * \right)$, với \(AN = \dfrac{{a\sqrt 3 }}{2};\,AC = a\sqrt 2 \) thay vào \(\left( * \right)\) ta được $AK = \dfrac{{a\sqrt {66} }}{{11}}$. Vậy $d\left( {M;\,\left( {NCD} \right)} \right) = \dfrac{1}{4}AK = \dfrac{{a\sqrt {66} }}{{44}}$
Cho hình hộp chữ nhật $ABCD.A'B'C'D'$, $AB = 6{\rm{cm}}$, $BC = BB' = 2{\rm{cm}}$. Điểm $E$ là trung điểm cạnh $BC$. Một tứ diện đều $MNPQ$ có hai đỉnh $M$ và $N$ nằm trên đường thẳng $C'E$, hai đỉnh $P$, $Q$ nằm trên đường thẳng đi qua điểm $B'$ và cắt đường thẳng $AD$ tại điểm $F$. Khoảng cách $DF$ bằng
Do tứ diện $MNPQ$ đều nên ta có $MN \bot PQ$ hay $EC' \bot B'F$.
Ta có: $\overrightarrow {B'F} = \overrightarrow {B'A} + \overrightarrow {AF} = \overrightarrow {B'A'} + \overrightarrow {B'B} + k\overrightarrow {AD} = \overrightarrow {B'A'} + \overrightarrow {B'B} + k\overrightarrow {B'C'} $
Và $\overrightarrow {EC'} = \overrightarrow {EC} + \overrightarrow {CC'} = \dfrac{1}{2}\overrightarrow {B'C'} - \overrightarrow {B'B} $
Khi đó, $\overrightarrow {EC'} .\overrightarrow {BF} = - B'{B^2} + \dfrac{k}{2}B'{C'^2} = - 4 + \dfrac{k}{2}.4 = 0$ $ \Rightarrow k = 2$.
Vậy $\overrightarrow {AF} = 2\overrightarrow {AD} $
Vậy $F$ là điểm trên $AD$ sao $D$ là trung điểm của $AF$.
Do đó $DF = BC = 2{\rm{cm}}$.
