Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông, cạnh bên \(SA\) vuông góc với mặt phẳng đáy. Đường thẳng \(SD\) tạo với mặt phẳng \(\left( {SAB} \right)\) một góc \(45^\circ \). Gọi \(I\) là trung điểm của cạnh \(CD\). Góc giữa hai đường thẳng \(BI\) và \(SD\) bằng (Số đo góc được làm tròn đến hàng đơn vị).
Trả lời bởi giáo viên
Đáp án đúng: b
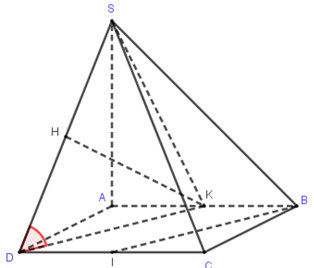
Giả sử hình vuông \(ABCD\) cạnh \(a\), \(\left( {\widehat {SD,\,\left( {SAB} \right)}} \right) = 45^\circ \)\( \Rightarrow SA = AD = a\)
Gọi \(K\) là trung điểm của \(AB\).
Vì \(KD\,{\rm{//}}\,BI\) nên góc giữa hai đường thẳng \(BI\) và \(SD\) bằng góc giữa hai đường thẳng \(KD\) và \(SD\) và là góc \(\widehat {SDK}\).
Ta có \(KD = SK = \dfrac{{a\sqrt 5 }}{2}\), \(SD = a\sqrt 2 \).
Gọi \(H\) là trung điểm của \(SD\). Ta có \(\cos \widehat {SDK} = \dfrac{{HD}}{{KD}} = \dfrac{{\dfrac{{a\sqrt 2 }}{2}}}{{\dfrac{{a\sqrt 5 }}{2}}} = \dfrac{{\sqrt {10} }}{5}\).
Vậy góc giữa hai đường thẳng \(BI\) và \(SD\) bằng \(51^\circ .\)
Hướng dẫn giải:
- Xác định góc giữa \(SD\) và mặt phẳng \(\left( {SAB} \right)\) (là góc giữa \(SD\) và hình chiếu của nó trên \(\left( {SAB} \right)\))
- Xác định góc giữa \(BI\) và \(SD\) sử dụng kiến thức:
Nếu \(b//c\) thì \(\widehat {\left( {a,b} \right)} = \widehat {\left( {a,c} \right)}\)
- Sử dụng các kiến thức hình học đã biết để tính số đo góc cần tìm.
