Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABCD\), đáy là hình thang vuông tại \(A\) và \(B\), biết \(AB = BC = a\), \(AD = 2a\), \(SA = a\sqrt 3 \) và \(SA \bot \left( {ABCD} \right)\). Gọi \(M\) và \(N\) lần lượt là trung điểm của \(SB\), \(SA\). Tính khoảng cách từ \(M\) đến \(\left( {NCD} \right)\) theo \(a\).
Trả lời bởi giáo viên
Đáp án đúng: d
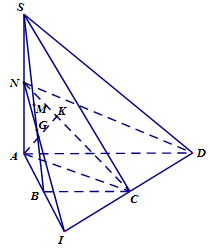
Gọi \(I\) là giao điểm của \(AB\) và \(CD\), vì \(AD = 2BC\) nên \(B\) là trung điểm của \(AI\).
Gọi \(G\) là giao điểm của \(SB\) và \(IN\), dễ thấy \(G\) là trọng tâm tam giác \(SAI\).
Do đó, \(SG = \dfrac{2}{3}SB = \dfrac{4}{3}SM \Rightarrow MG = \dfrac{1}{4}SG\), mà \(G \in \left( {NCD} \right)\) nên $d\left( {M;\,\left( {NCD} \right)} \right) = \dfrac{1}{4}d\left( {S;\,\left( {NCD} \right)} \right) = \dfrac{1}{4}d\left( {A;\,\left( {NCD} \right)} \right)$.
Lại có, \(CD \bot AC;\,CD \bot SA \Rightarrow CD \bot \left( {SAC} \right)\).
Gọi \(K\) là hình chiếu của \(A\) lên \(NC\) thì $d\left( {A;\,\left( {NCD} \right)} \right) = AK = \dfrac{{AN.AC}}{{\sqrt {A{N^2} + A{C^2}} }}\,\,\,\left( * \right)$, với \(AN = \dfrac{{a\sqrt 3 }}{2};\,AC = a\sqrt 2 \) thay vào \(\left( * \right)\) ta được $AK = \dfrac{{a\sqrt {66} }}{{11}}$. Vậy $d\left( {M;\,\left( {NCD} \right)} \right) = \dfrac{1}{4}AK = \dfrac{{a\sqrt {66} }}{{44}}$
Hướng dẫn giải:
- Gọi \(I\) là giao điểm của \(AB\) và \(CD\) rồi xác định giao điểm của \(SB\) với \(\left( {NCD} \right)\)
- Tính khoảng cách từ \(M\) đến \(\left( {NCD} \right)\) sử dụng kiến thức:
