Câu hỏi:
3 năm trước
Cho hình chóp \(S.ABC\) có \(AB = AC\), \(\widehat {SAC} = \widehat {SAB}\). Tính số đo của góc giữa hai đường thẳng \(SA\) và \(BC.\)
Trả lời bởi giáo viên
Đáp án đúng: d
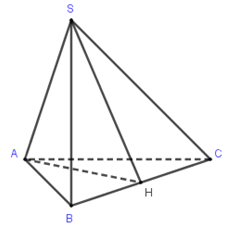
Vì \(AB = AC\), \(\widehat {SAC} = \widehat {SAB}\) nên \(\Delta \,SAC = \Delta \,SAB\), suy ra \(SB = SC\), nên hai tam giác \(ABC\) và \(SBC\) là tam giác cân. Gọi \(H\) là trung điểm \(BC\), ta có \(\left\{ \begin{array}{l}AH \bot BC\\SH \bot BC\end{array} \right. \Rightarrow \left( {SAH} \right) \bot BC\).
Vậy \(SA \bot BC\).
Hướng dẫn giải:
Dựa vào các điều kiện bài cho tìm mối quan hệ góc, độ dài của các cạnh hình chóp, từ đó suy ra góc giữa hai đường thẳng.

