Câu hỏi:
3 năm trước
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành, cạnh bên \(SA\) vuông góc với đáy. Biết khoảng cách từ \(A\) đến \(\left( {SBD} \right)\) bằng \(\dfrac{{6a}}{7}\). Tính khoảng cách từ \(C\) đến mặt phẳng \(\left( {SBD} \right)\)?
Trả lời bởi giáo viên
Đáp án đúng: d
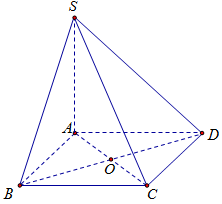
Do \(ABCD\) là hình bình hành\( \Rightarrow AC \cap BD = O\) là trung điểm của \(AC\) và \(BD\)\( \Rightarrow d\left( {C,\left( {SBD} \right)} \right) = d\left( {A,\left( {SBD} \right)} \right) = \dfrac{{6a}}{7}\).
Hướng dẫn giải:
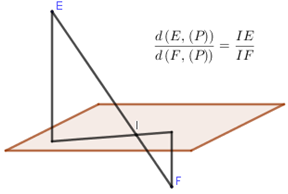
Sử dụng tính chất dưới đây: