Câu hỏi:
2 năm trước
Cho hình chóp $S.ABCD$ có tất cả các cạnh bên và cạnh đáy đều bằng $a$ và $ABCD$ là hình vuông. Gọi $M$ là trung điểm của $CD.$ Giá trị \(\overrightarrow {MS} .\overrightarrow {CB} \) bằng
Trả lời bởi giáo viên
Đáp án đúng: a
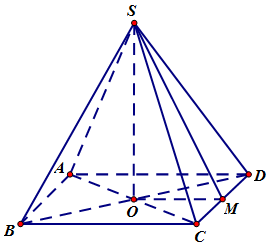
Do tất cả các cạnh của hình chóp bằng nhau nên hình chóp \(S.ABCD\) là hình chóp đều \( \Rightarrow \left\{ \begin{array}{l}SO \bot (ABCD)\\AC \bot BD\end{array} \right.\).
Do M là trung điểm của CD nên ta có:
\(\overrightarrow {MS} = \overrightarrow {{\rm{O}}S} - \overrightarrow {OM} = - \dfrac{1}{2}\overrightarrow {OC} - \dfrac{1}{2}\overrightarrow {OD} + \overrightarrow {{\rm{O}}S} \), \(\overrightarrow {CB} = \overrightarrow {OB} - \overrightarrow {OC} = - \overrightarrow {OD} - \overrightarrow {OC} \).
Do \(\overrightarrow {OC} ;\) \(\overrightarrow {OS} ;\) \(\overrightarrow {OD} \) đôi một vuông góc với nhau nên ta có:
\(\overrightarrow {MS} .\overrightarrow {CB} = \dfrac{1}{2}O{C^2} + \dfrac{1}{2}O{D^2} = O{C^2} = \dfrac{{{a^2}}}{2}\)
Hướng dẫn giải:
Biểu diễn các véc tơ \(\overrightarrow {MS} ,\overrightarrow {CB} \) theo ba véc tơ đôi một vuông góc \(\overrightarrow {OC} ,\overrightarrow {OD} ,\overrightarrow {OS} \) rồi thực hiện nhân hai véc tơ.
