Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABC\) có \(SA = SB = SC = AB = AC = a\), \(BC = a\sqrt 2 \). Tính số đo của góc giữa hai đường thẳng \(AB\) và \(SC\) ta được kết quả:
Trả lời bởi giáo viên
Đáp án đúng: c
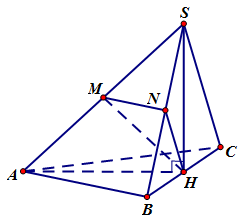
Gọi $H$ là hình chiếu vuông góc của $S$ lên mặt phẳng \(\left( {ABC} \right)\), theo đầu bài \(SA = SB = SC\) và tam giác \(\Delta ABC\) vuông cân tại \(A\) ta có \(H\) là trung điểm của \(BC\). Gọi \(M\), \(N\) lần lượt là trung điểm của \(SA\), \(SB\) ta có: \(\left\{ \begin{array}{l}MN\;{\rm{//}}\;AB\\HN\;{\rm{//}}\;SC\end{array} \right.\)
\( \Rightarrow \) Góc giữa \(AB\) và \(SC\) là góc giữa \(MN\) và \(HN\).
Xét tam giác \(\Delta MNH\) ta có: \(MN = \dfrac{{AB}}{2} = \dfrac{a}{2};\) \(HN = \dfrac{{SC}}{2} = \dfrac{a}{2}\;;\) \(MH = \dfrac{{SA}}{2} = \dfrac{a}{2}\)
(do \(\Delta SHA\) vuông tại \(H\))
\( \Rightarrow \) tam giác \(\Delta MNH\) là tam giác đều \( \Rightarrow \)\(\widehat {MNH} = 60^\circ \).
Vậy góc cần tìm là \(60^\circ \).
Hướng dẫn giải:
Sử dụng kiến thức:
Nếu \(\left\{ \begin{array}{l}a//b\\c//d\end{array} \right.\) thì \(\widehat {\left( {a,c} \right)} = \widehat {\left( {b,d} \right)}\)
Do đó tìm hai đường thẳng lần lượt song song với \(AB,SC\) mà dễ dàng xác định góc rồi kết luận.
