Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật với \(AB = 2a\), \(BC = a\). Các cạnh bên của hình chóp cùng bằng $a\sqrt 2 $. Tính góc giữa hai đường thẳng \(AB\) và \(SC\).
Trả lời bởi giáo viên
Đáp án đúng: a
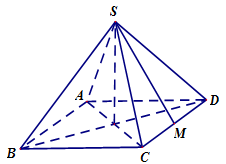
Ta có \(AB{\rm{//}}CD\) nên $\left( {\widehat {AB;\,SC}} \right) = \left( {\widehat {CD;\,SC}} \right) = \widehat {SCD}$.
Gọi \(M\) là trung điểm của \(CD\).
Tam giác \(SCM\) vuông tại \(M\) và có \(SC = a\sqrt 2 \), \(CM = a\) nên là tam giác vuông cân tại \(M\) nên $\widehat {SCD} = 45^\circ $.
Vậy $\left( {\widehat {AB;\,SC}} \right) = 45^\circ $.
Hướng dẫn giải:
- Sử dụng kiến thức: \(b//c \Rightarrow \widehat {\left( {a,b} \right)} = \widehat {\left( {a,c} \right)}\) để xác định góc của hai đường thẳng
- Sử dụng kiến thức hình học đã biết để tìm độ lớn của góc đó.
