Câu hỏi:
2 năm trước
Cho hình lăng trụ đứng $ABC.A'B'C'$ có đáy là tam giác $ABC$ vuông tại $A$ có $BC = 2a$, $AB = a\sqrt 3 $. Khoảng cách từ $AA'$ đến mặt phẳng $\left( {BCC'B'} \right)$ là:
Trả lời bởi giáo viên
Đáp án đúng: b
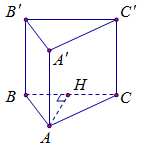
Ta có $AA'{\rm{//}}\left( {BCC'B'} \right)$ nên khoảng cách từ $AA'$ đến mặt phẳng $\left( {BCC'B'} \right)$ cũng chính là khoảng cách từ $A$ đến mặt phẳng $\left( {BCC'B'} \right)$.
Hạ $AH \bot BC \Rightarrow AH \bot \left( {BCC'B'} \right)$.
Ta có $\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}} = \dfrac{1}{{3{a^2}}} + \dfrac{1}{{B{C^2} - A{B^2}}} = \dfrac{1}{{3{a^2}}} + \dfrac{1}{{{a^2}}} = \dfrac{4}{{3{a^2}}}$$ \Rightarrow AH = \dfrac{{a\sqrt 3 }}{2}$.
Vậy khoảng cách từ $AA'$ đến mặt phẳng $\left( {BCC'B'} \right)$ bằng $\dfrac{{a\sqrt 3 }}{2}$.
Hướng dẫn giải:
Sử dụng kiến thức:
Cho \(a//\left( P \right)\) thì \(d\left( {a,\left( P \right)} \right) = d\left( {A,\left( P \right)} \right)\) với \(A \in a\)
