Câu hỏi:
3 năm trước
Cho hình chóp $S.ABCD$có đáy $ABCD$ là hình vuông cạnh $a$, cạnh bên $SA$ vuông góc với mặt đáy và \(SA = a\sqrt 2 \). Tìm số đo của góc giữa đường thẳng $SC$ và mặt phẳng$\left( {SAB} \right)$.
Trả lời bởi giáo viên
Đáp án đúng: b
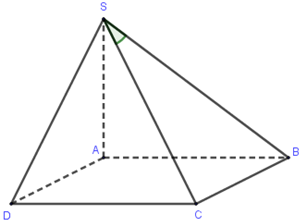
Dễ thấy $CB \bot \left( {SAB} \right)$ $ \Rightarrow SB$ là hình chiếu vuông góc của $SC$ lên $\left( {SAB} \right)$.
Vậy góc giữa đường thẳng $SC$ và mặt phẳng $\left( {SAB} \right)$ là $\widehat {CSB}$.
Tam giác $CSB$ có $\widehat B = 90^\circ ;\,CB = a;\,SB = a\sqrt 3 \Rightarrow \tan \widehat {CSB} = \dfrac{{CB}}{{SB}} = \dfrac{a}{{a\sqrt 3 }} = \dfrac{1}{{\sqrt 3 }}$.
Vậy $\widehat {CSB}$ \( = 30^\circ \).
Hướng dẫn giải:
Góc giữa đường thẳng và mặt phẳng (khác \({90^0}\)) là góc giữa đường thẳng đó với hình chiếu của nó trên mặt phẳng.

