Câu hỏi:
2 năm trước
Cho ba điểm \(A\), \(B\), \(C\) thẳng hàng theo thứ tự đó và \(AB = 2BC\). Dựng các hình vuông \(ABEF\), \(BCGH\) (đỉnh của hình vuông tính theo chiều kim đồng hồ). Xét phép quay tâm \(B\) góc quay \( - 90^\circ \) biến điểm \(E\) thành điểm \(A.\) Gọi \(I\) là giao điểm của \(EC\) và \(GH.\) Giả sử \(I\) biến thành điểm \(J\) qua phép quay trên. Nếu \(AC = 3\) thì \(IJ\) bằng
Trả lời bởi giáo viên
Đáp án đúng: d
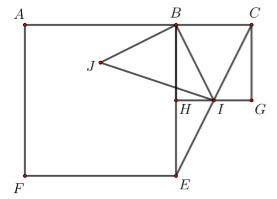
Do \(Q\left( {B; - 90^\circ } \right):I \to J\) nên \(\Delta BIJ\) vuông cân tại \(B\) \( \Rightarrow IJ = BI\sqrt 2 \).
Mà \(AC = 3\) \( \Rightarrow BC = 1\). Vì \(AB = 2BC\) \( \Rightarrow BE = 2BH\) \( \Rightarrow \) \(HI\) là đường trung bình \(\Delta EBC\)
\( \Rightarrow HI = \dfrac{1}{2}BC = \dfrac{1}{2}\). Ta có \(BI = \sqrt {B{H^2} + I{H^2}} = \sqrt {1 + \dfrac{1}{4}} = \dfrac{{\sqrt 5 }}{2}\)
Vậy $IJ = BH\sqrt 2 = \dfrac{{\sqrt {10} }}{2}$.
Hướng dẫn giải:
Dựng hình và tính độ dài \(IJ\) sử dụng các kiến thức hình học đã biết.
