Câu hỏi:
2 năm trước
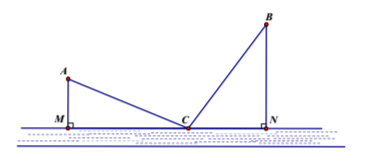
Thành phố Hải Đông dự định xây dựng một trạm nước sạch để cung cấp cho hai khu dân cư \(A\) và \(B\). Trạm nước sạch đặt tại vị trí\(C\) trên bờ sông. Biết \(AB = 3\sqrt {17} \,{\rm{km}}\), khoảng cách từ \(A\) và \(B\) đến bờ sông lần lượt là \(AM = 3\,{\rm{km}}\), \(BN = 6\,{\rm{km}} \)(hình vẽ). Gọi \(T\) là tổng độ dài đường ống từ trạm nước đến \(A\) và \(B\). Tìm giá trị nhỏ nhất của \(T\).
Trả lời bởi giáo viên
Đáp án đúng: a
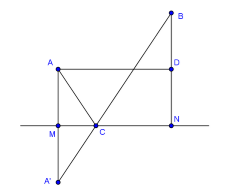
Gọi \(A'\) đối xứng với\(A\) qua \(MN\), \(D\) là trung điểm của \(NB\).
Do \(A\) cố định nên \(A'\) cũng cố định.
Ta có: \(T = CA + CB = CA' + CB \ge A'B\) (không đổi).
Đẳng thức xảy ra khi \(\left\{ C \right\} = MN \cap A'B\).
Khi đó: \(\dfrac{{MC}}{{NC}} = \dfrac{{MA'}}{{NB}} = \dfrac{{MA}}{{NB}} = \dfrac{1}{2}\) (1)
Mặt khác, \(MN = AD = \sqrt {A{B^2} - D{B^2}} \) \(= \sqrt {153 - 9} = 12 \,{\rm{km}}\) (2)
Từ (1) và (2) suy ra \(MC = 4\,km\), \(NC = 8 \,{\rm{km}}\).
Vậy \(T = CA + CB = \sqrt {A{M^2} + M{C^2}} + \sqrt {B{N^2} + N{C^2}}\) \( = \sqrt {9 + 16} + \sqrt {36 + 64} = 15\,{\rm{km}}\).
Hướng dẫn giải:
Lấy \(A'\) đối xứng với \(A\) qua \(M\), từ đó nhận xét giá trị nhỏ nhất của \(AC + CB\)
