Cho hình chóp $S.ABC$ đáy $ABC$ là tam giác vuông cân với $BA = BC = a$, $SA = a$ và vuông góc với đáy, cosin góc giữa hai mặt phẳng $\left( {SAC} \right)$ và $\left( {SBC} \right)$ bằng:

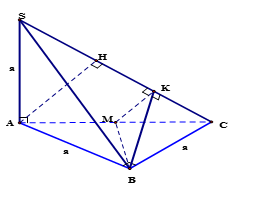
Cách 1:

Trong $\Delta SAC$, vẽ $AH \bot SC$

Gọi $M$ là trung điểm của $AC$, vẽ $MK \bot SC$ (1)

Vì $\Delta BAC$ vuông cân tại $B$ $ \Rightarrow $ $BM \bot AC$

Theo giả thiết $SA \bot \left( {ABC} \right) \Rightarrow SA \bot BM$

Ta có $\left\{ \begin{array}{l}BM \bot AC\\BM \bot SA\end{array} \right. \Rightarrow BM \bot \left( {SAC} \right) \Rightarrow BM \bot SC$ (2)

Từ (1) và (2) $ \Rightarrow $ $SC \bot \left( {BMK} \right) \Rightarrow SC \bot BK$ (3)

Từ (1) và (3) $ \Rightarrow $ $\left\{ \begin{array}{l}MK \bot SC;\,\,MK \subset \left( {SAC} \right)\\SC \bot BK;\,\,BK \subset \left( {SBC} \right)\end{array} \right.$

$ \Rightarrow $ $\left( {\left( {SAC} \right);\,\left( {SBC} \right)} \right) = \left( {BK;\,MK} \right) = \widehat {BKM}$

Vì tam giác $SBC$ vuông tại $B$, nên $\dfrac{1}{{B{K^2}}} = \dfrac{1}{{B{C^2}}} + \dfrac{1}{{B{A^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{2{a^2}}} = \dfrac{3}{{2{a^2}}}\,\,\, \Rightarrow BK = \dfrac{{a\sqrt 6 }}{3}$

Vì $\Delta MCK \sim \Delta SCA$ $ \Rightarrow $ $\dfrac{{MK}}{{SA}} = \dfrac{{MC}}{{SC}} \Leftrightarrow MK = \dfrac{{MC.SA}}{{SC}} = \dfrac{{\dfrac{{a\sqrt 2 }}{2}.a}}{{a\sqrt 3 }} = \dfrac{{a\sqrt 6 }}{6}$

Theo CMT, ta có $BM \bot \left( {SAC} \right)$ $ \Rightarrow $ $BM \bot MK$ $ \Rightarrow $ $\Delta BMK$ vuông tại $M$

Do đó, $\cos \widehat {BMK} = \dfrac{{MK}}{{BK}} = \dfrac{{a\sqrt 6 }}{6}:\dfrac{{a\sqrt 6 }}{3} = \dfrac{1}{2}$