Câu hỏi:
2 năm trước
Cho hình chóp tứ giác đều có cạnh đáy bằng \(a\) và chiều cao bằng $\dfrac{{a\sqrt 3 }}{2}$. Tính số đo của góc giữa mặt bên và mặt đáy.
Trả lời bởi giáo viên
Đáp án đúng: d
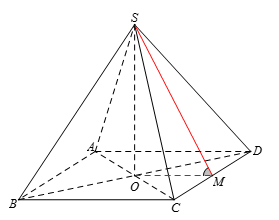
Gọi $O$ là tâm hình vuông $ABCD$, $M$ là trung điểm $CD$.
\(\left\{ \begin{array}{l}\left( {SCD} \right) \cap \left( {ABCD} \right) = CD\\SM \subset \left( {SCD} \right):{\rm{ }}SM \bot CD\\OM \subset \left( {ABCD} \right):{\rm{ }}OM \bot CD\end{array} \right.\) \( \Rightarrow \left( {\widehat {\left( {SCD} \right),\left( {ABCD} \right)}} \right) = \left( {\widehat {SM,OM}} \right) = \widehat {SMO}\).
$\tan \widehat {SMO} = \dfrac{{SO}}{{OM}} = \dfrac{{\dfrac{{a\sqrt 3 }}{2}}}{{\dfrac{a}{2}}} = \sqrt 3 $ $ \Rightarrow \widehat {SMO} = 60^\circ $.
Hướng dẫn giải:
Xác định góc giữa hai mặt phẳng: là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng mà cùng vuông góc với giao tuyến.
