Câu hỏi:
3 năm trước
Cho hình chóp $S.ABC$ có tam giác $ABC$ vuông cân tại $B$, $AB = BC = a$, $SA = a\sqrt 3 $, $SA \bot \left( {ABC} \right)$. Góc giữa hai mặt phẳng $\left( {SBC} \right)$ và $\left( {ABC} \right)$ là
Trả lời bởi giáo viên
Đáp án đúng: b
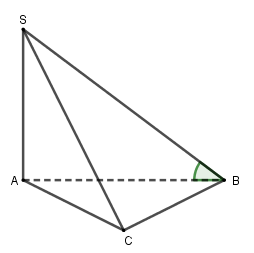
Ta có $BC \bot \left( {SAB} \right)$$ \Rightarrow BC \bot SA$. Góc giữa hai mặt phẳng $\left( {SBC} \right)$ và $\left( {ABC} \right)$ là góc $\widehat {SBA}$. $\tan \widehat {SBA} = \dfrac{{SA}}{{AB}}$$ = \dfrac{{a\sqrt 3 }}{a}$$ = \sqrt 3 $$ \Rightarrow \widehat {SBA} = 60^\circ $.
Hướng dẫn giải:
Xác định góc \(\alpha \) bằng cách sử dụng lý thuyết: Góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng lần lượt nằm trong hai mặt phẳng mà vuông góc với giao tuyến.

