Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại đỉnh \(A\), cạnh \(BC = a\), \(AC = \dfrac{{a\sqrt 6 }}{3}\) các cạnh bên \(SA = SB = SC = \dfrac{{a\sqrt 3 }}{2}\). Tính góc tạo bởi mặt bên \(\left( {SAB} \right)\) và mặt phẳng đáy \(\left( {ABC} \right)\).
Trả lời bởi giáo viên
Đáp án đúng: b
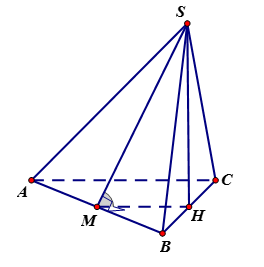
Vì \(SA = SB = SC = \dfrac{{a\sqrt 3 }}{2}\) nên hình chiếu của \(S\) trùng với \(H\) là tâm đường tròn ngoại tiếp đáy \(ABC\). Nhận xét \(H\) là trung điểm \(BC\).
Gọi \(M\) là trung điểm \(AB\), nhận xét \(AB \bot \left( {SMH} \right)\) nên góc tạo bởi mặt bên \(\left( {SAB} \right)\) và mặt phẳng đáy \(\left( {ABC} \right)\) là góc \(\widehat {SMH}\).
Xét tam giác \(SBH\) có \(SH = \sqrt {S{B^2} - B{H^2}} = \dfrac{{a\sqrt 2 }}{2}\).
Xét tam giác \(SMH\) có \(\tan \widehat M = \dfrac{{SH}}{{MH}} = \dfrac{{\dfrac{{a\sqrt 2 }}{2}}}{{\dfrac{{a\sqrt 6 }}{6}}} = \sqrt 3 \) \( \Leftrightarrow \widehat M = {60^{\rm{o}}}\).
Hướng dẫn giải:
Xác định góc giữa hai mặt phẳng: là góc giữa hai đường thẳng lần lượt nằm trong hai mặt phẳng mà cùng vuông góc với giao tuyến.
Khối chóp S.ABC có SA=SB=SC thì hình chiếu của S lên đáy là tâm đường tròn ngoại tiếp đáy ABC.
