Câu hỏi:
2 năm trước
Cho tứ diện \(S.ABC\) có các cạnh \(SA\), \(SB\); \(SC\) đôi một vuông góc và \(SA = SB = SC = 1\). Tính \(\cos \alpha \), trong đó \(\alpha \) là góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABC} \right)\)?
Trả lời bởi giáo viên
Đáp án đúng: d
Cách 1:
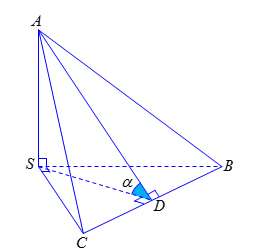
Gọi \(D\) là trung điểm cạnh \(BC\).
Ta có \(\left\{ \begin{array}{l}SA \bot SB\\SA \bot SC\end{array} \right. \Rightarrow SA \bot \left( {SBC} \right)\)\( \Rightarrow SA \bot BC\).
Mà \(SD \bot BC\) nên \(BC \bot \left( {SAD} \right)\).
\( \Rightarrow \left( {\widehat {\left( {SBC} \right),\left( {ABC} \right)}} \right) = \widehat {SDA} = \alpha \).
Khi đó tam giác \(SAD\) vuông tại \(S\) có \(SD = \dfrac{1}{{\sqrt 2 }}\); \(AD = \dfrac{{\sqrt 3 }}{{\sqrt 2 }}\) và \(\cos \alpha = \dfrac{{SD}}{{AD}}\) \( \Leftrightarrow \cos \alpha = \dfrac{1}{{\sqrt 3 }}\).
Hướng dẫn giải:
Xác định góc \(\alpha \) bằng cách sử dụng lý thuyết: Góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng lần lượt nằm trong hai mặt phẳng mà vuông góc với giao tuyến.
