Câu hỏi:
2 năm trước
Giả sử $\alpha $ là góc của hai mặt của một tứ diện đều có cạnh bằng $a$. Khẳng định đúng là
Trả lời bởi giáo viên
Đáp án đúng: a
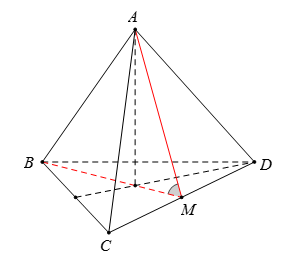
Gọi $M$ là trung điểm cạnh $CD$ của tứ diện đều $ABCD$.
Ta có $\left\{ \begin{array}{l}\left( {ACD} \right) \cap \left( {BCD} \right) = CD\\AM \subset \left( {ACD} \right):AM \bot CD\\BM \subset \left( {BCD} \right):BM \bot CD\end{array} \right.$ $ \Rightarrow $ $\left( {\widehat {\left( {ACD} \right),\left( {BCD} \right)}} \right) = \left( {\widehat {AM,BM}} \right) = \widehat {AMB} = \alpha $.
Tính: $AB = a$, $AM = BM = \dfrac{{a\sqrt 3 }}{2}$.
$cos\alpha = \cos \widehat {AMB} = \dfrac{{A{M^2} + B{M^2} - A{B^2}}}{{2.AM.BM}} = \dfrac{{2.{{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2} - {a^2}}}{{2.\dfrac{{a\sqrt 3 }}{2}.\dfrac{{a\sqrt 3 }}{2}}} = \dfrac{1}{3}$.
$ \Rightarrow {\tan ^2}\alpha = \dfrac{1}{{{{\cos }^2}\alpha }} - 1 = 8 \Rightarrow \tan \alpha = \sqrt 8 $.
Hướng dẫn giải:
Xác định góc giữa hai mặt phẳng: là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng mà cùng vuông góc với giao tuyến.
