Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABCD\) đáy \(ABCD\) là hình chữ nhật, \(AB = a\), \(AD = 2a\). Cạnh bên \(SA\) vuông góc với đáy \(\left( {ABCD} \right)\), \(SA = 2a\). Tính \(\tan \) của góc giữa hai mặt phẳng \(\left( {SBD} \right)\) và \(\left( {ABCD} \right)\).
Trả lời bởi giáo viên
Đáp án đúng: c
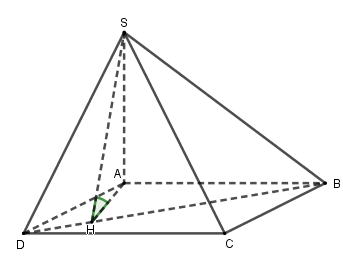
Kẻ \(AH \bot BD\), \(\left( {H \in BD} \right)\) (1).
\(\left\{ \begin{array}{l}BD \bot SA\,\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\\BD \bot AH\end{array} \right.\) \( \Rightarrow BD \bot \left( {SAH} \right)\) \( \Rightarrow BD \bot SH\) (2).
Và: \(\left( {SBD} \right) \cap \left( {ABCD} \right) = BD\) (3).
Từ (1) (2) và (3) suy ra: Góc giữa hai mặt phẳng \(\left( {SBD} \right)\) và \(\left( {ABCD} \right)\)là \(\widehat {SHA}\).
Xét \(\Delta ABD\) vuông tại \(A\): \(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{D^2}}}\)\( = \dfrac{1}{{{a^2}}} + \dfrac{1}{{4{a^2}}}\)\( = \dfrac{5}{{4{a^2}}}\) $ \Rightarrow AH = \dfrac{{2a}}{{\sqrt 5 }}$.
Xét \(\Delta SAH\) vuông tại \(A\): \(\tan \widehat {SHA} = \dfrac{{SA}}{{AH}} = \sqrt 5 \).
Hướng dẫn giải:
Xác định góc giữa hai mặt phẳng: bằng góc giữa hai đường thẳng lần lượt nằm trong hai mặt phẳng mà cùng vuông góc với giao tuyến.
