Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\), \(AB = 2a\), \(AD = DC = a\), \(SA = \,a\sqrt 2 \), \(SA \bot \left( {ABCD} \right)\). Tính cosin của góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {SCD} \right)\).
Trả lời bởi giáo viên
Đáp án đúng: c
Cách 1:
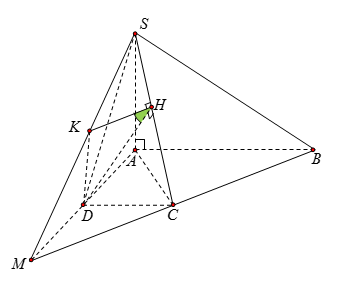
Gọi \(M = BC \cap AD\). Khi đó: \(\left( {\widehat {\left( {SBC} \right),\left( {SCD} \right)}} \right) = \left( {\widehat {\left( {SCM} \right),\left( {SCD} \right)}} \right)\)
Gọi \(H\) là hình chiếu của \(D\) lên \(SC\), kẻ \(HK\,{\rm{//}}\,MC\)\(\left( {K \in SM} \right)\) ta có:
\(\left( {\widehat {\left( {SCM} \right),\left( {SCD} \right)}} \right) = \widehat {KHD} = \alpha \)
Xét \(\Delta SCD\) vuông tại \(D\) ta có: \(\dfrac{1}{{D{H^2}}} = \dfrac{1}{{D{C^2}}} + \dfrac{1}{{D{S^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{3{a^2}}} = \dfrac{4}{{3{a^2}}}\)\( \Rightarrow DH = \dfrac{{a\sqrt 3 }}{2}\).
\(HC = \dfrac{{D{C^2}}}{{SC}} = \dfrac{{{a^2}}}{{2a}} = \dfrac{a}{2}\).
Do \(HK\,{\rm{//}}\,MC\) mà \(\dfrac{{SH}}{{SC}} = \dfrac{3}{4}\) nên \(HK = \dfrac{3}{4}a\sqrt 2 = \dfrac{{3\sqrt 2 a}}{4}\); \(KM = \dfrac{1}{4}SM = \dfrac{{a\sqrt 6 }}{4}\).
Mặt khác ta có: \(\widehat {KDM} = \widehat {DSA}\) mà \(\sin \widehat {KMD} = \sin \widehat {DSA} = \dfrac{1}{{\sqrt 3 }}\) nên \(\widehat {KDM} = \widehat {KMD}\).
Do đó: \(KD = KM = \dfrac{{a\sqrt 6 }}{4}\).
Xét tam giác \(KDH\) ta có: \(\cos \alpha = \dfrac{{H{D^2} + H{K^2} - K{D^2}}}{{2HK.HD}} = \dfrac{{\sqrt 6 }}{3}\).
Hướng dẫn giải:
- Xác định giao tuyến của hai mặt phẳng.
- Dựng các đường thẳng lần lượt vuông góc với giao tuyến mà nằm trong hai mặt phẳng.
- Góc giữa hai mặt phẳng bằng góc giữa hai giao tuyến trên.
- Tính góc dựa vào các kiến thức hình học đã biết.
