Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\). Cạnh bên \(SA\) vuông góc với mặt phẳng đáy và có độ dài bằng \(a\sqrt 2 \). Gọi \(\alpha \) là góc giữa hai mặt phẳng \(\left( {SAD} \right)\) và \(\left( {SBD} \right)\). Tính \(\cos \alpha \).
Trả lời bởi giáo viên
Đáp án đúng: d
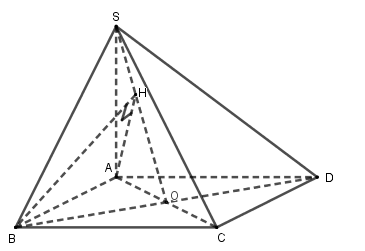
Gọi \(O\) là tâm hình vuông \(ABCD\). Kẻ \(AH \bot SO\) tại \(H\).
Ta có: \(BD \bot AO,\) \(BD \bot SA\)\( \Rightarrow BD \bot \left( {SAO} \right)\)\( \Rightarrow BD \bot AH\). Vậy \(AH \bot \left( {SBD} \right)\).
Lại có: \(AB \bot \left( {SAD} \right)\), do đó góc \(\alpha \) giữa hai mặt phẳng \(\left( {SAD} \right)\) và \(\left( {SBD} \right)\) là góc giữa hai đường thẳng \(AH\) và \(AB\). Do đó \(\alpha = \widehat {BAH}\) và \(\widehat {BAH} < {90^0} = \widehat {BHA}\).
Tam giác \(SAO\) vuông tại \(A\), đường cao \(AH\) nên: \(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{S^2}}} + \dfrac{1}{{A{O^2}}} = \dfrac{1}{{2{a^2}}} + \dfrac{4}{{2{a^2}}} = \dfrac{5}{{2{a^2}}}\)
Suy ra: \(AH = \dfrac{{a\sqrt {10} }}{5}\). Từ đó: \(\cos \alpha = \dfrac{{AH}}{{AB}} = \dfrac{{\sqrt {10} }}{5}\).
Hướng dẫn giải:
Xác định góc giữa hai mặt phẳng: là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
Áp dụng: Tìm hai đường thẳng lần lượt vuông góc với hai mặt phẳng \(\left( {SAD} \right)\) và \(\left( {SBD} \right)\) rồi xác định góc.
