Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác cân, với\(AB = AC = a\) và góc \(\widehat {BAC} = 120^\circ \), cạnh bên \(AA' = a\). Gọi \(I\) là trung điểm của \(CC'\). Cosin của góc tạo bởi hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {AB'I} \right)\) bằng

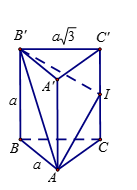
Ta có \(B{C^2} = A{B^2} + A{C^2} - 2AB.AC.\cos \widehat {BAC}\)\( = {a^2} + {a^2} - 2.a.a.\left( { - \dfrac{1}{2}} \right)\)\( = 3{a^2}\)\( \Rightarrow BC = a\sqrt[{}]{3}\).

Xét tam giác vuông \(B'AB\) có \(AB' = \sqrt[{}]{{B{{B'}^2} + A{B^2}}}\)\( = \sqrt[{}]{{{a^2} + {a^2}}}\)\( = a\sqrt[{}]{2}\).

Xét tam giác vuông \(IAC\) có \(IA = \sqrt[{}]{{I{C^2} + A{C^2}}}\)\( = \sqrt[{}]{{{a^2} + \dfrac{{{a^2}}}{4}}}\)\( = \dfrac{{a\sqrt[{}]{5}}}{2}\).

Xét tam giác vuông \(IB'C'\) có \(B'I = \sqrt[{}]{{B'{{C'}^2} + C'{I^2}}}\)\( = \sqrt[{}]{{3{a^2} + \dfrac{{{a^2}}}{4}}}\)\( = \dfrac{{a\sqrt[{}]{{13}}}}{2}\).

Xét tam giác \(IB'A\) có \(B'{A^2} + I{A^2} = 2{a^2} + \dfrac{{5{a^2}}}{4}\)\( = \dfrac{{13{a^2}}}{4}\)\( = B'{I^2}\)\( \Rightarrow \Delta IB'A\) vuông tại $A$

\( \Rightarrow \)${S_{IB'A}} = \dfrac{1}{2}AB'.AI$$ = \dfrac{1}{2}.a\sqrt[{}]{2}.\dfrac{{a\sqrt[{}]{5}}}{2}$$ = \dfrac{{{a^2}\sqrt[{}]{{10}}}}{4}$.

Lại có \({S_{ABC}} = \dfrac{1}{2}AB.AC.\sin \widehat {BAC}\)\( = \dfrac{1}{2}a.a.\dfrac{{\sqrt[{}]{3}}}{2}\)\( = \dfrac{{{a^2}\sqrt[{}]{3}}}{4}\).

Gọi góc tạo bởi hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {AB'I} \right)\)là \(\alpha \).

Ta có \(\Delta ABC\) là hình chiếu vuông góc của \(\Delta AB'I\) trên mặt phẳng \(\left( {ABC} \right)\).

Do đó \({S_{ABC}} = {S_{IB'A}}.\cos \alpha \)\( \Rightarrow \dfrac{{{a^2}\sqrt[{}]{3}}}{4} = \dfrac{{{a^2}\sqrt[{}]{{10}}}}{4}.\cos \alpha \)$ \Rightarrow \cos \alpha  = \dfrac{{\sqrt[{}]{{30}}}}{{10}}$.