Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABC\) có \(SA \bot (ABC),\,SA = 2a.\) Tam giác\(ABC\)vuông tại B \(\,AB = a\), \(BC = a\sqrt 3 \). Tính cosin của góc \(\varphi \) tạo bởi hai mặt phẳng \((SAC)\) và \((SBC).\)
Trả lời bởi giáo viên
Đáp án đúng: a
Cách 1:
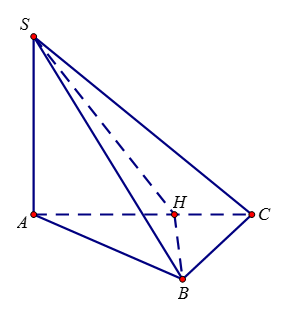
Kẻ \(BH \bot AC\,\,\,\,\, \Rightarrow BH \bot (SAC)\). Áp dụng công thức \(S' = S\cos \phi \) trong đó \(S' = dt\left( {SHC} \right)\),
\(S = dt\left( {SBC} \right)\), \(\phi \) là góc hợp bởi hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {SAC} \right)\)
Dễ thấy tam giác \(SBC\) vuông tại B và \(SB = a\sqrt 5 \). \(dt\left( {SBC} \right) = \dfrac{{{a^2}\sqrt {15} }}{2}\)
\(CH = \dfrac{{B{C^2}}}{{AC}} = \dfrac{3}{2}a\), \(dt\left( {SHC} \right) = \dfrac{3}{2}{a^2}\). Vậy \(\cos \phi = \dfrac{{\sqrt {15} }}{5}\)
Hướng dẫn giải:
Sử dụng lý thuyết:
Cho hình \(H\) nằm trong mặt phẳng \(\left( P \right)\) có diện tích \(S\), gọi \(H'\) là hình chiếu của \(H\) trên mặt phẳng \(\left( {P'} \right)\) tạo với \(\left( P \right)\) một góc \(\alpha \). Khi đó \(S' = S.\cos \alpha \).
